Fractals: A Different Type of Geometry
The Dimensions in Between
The mathematics that we have learned since elementary school is a bit beautiful. A line is perfectly straight, the path of the ball thrown upward is a parabola and the shape of the earth we see in books is a sphere. The truth is, the lines, parabolas, and spheres are “flawless models” of the real world. A straight line that can be drawn using a ruler or a meter stick is not perfectly straight (try using a magnifier). The shape of the path of the ball thrown upward is not all the time a symmetric parabola. Lastly, Earth is not a perfect sphere, it bulges in the equator, it has mountains, valleys, and trenches.
Clearly, the perfect mathematics that we know is an ideal notion and it does not have a very close resemblance of reality. It also appears that the mathematics, particularly the Geometry that we have learned in school is not enough to describe the real world. The dimensions that we have talked in the last post, cannot simply apply to these types of “irregularities.”
The Dimensions in Between
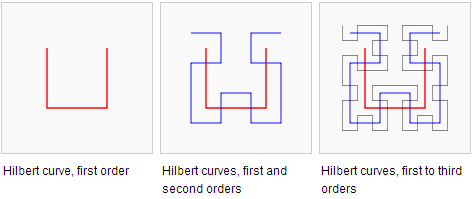
One of the amazing concepts explored by mathematicians in the 19th century is finding a curve (a path with length and no thickness and therefore 1 dimension) that can fill a two dimensional space.
The figure above is an example of such curve, the three orders of which are shown. Notice that the figures are similar, the basic shapes remain. Observe that as the paths are drawn with a finer scale, the amount of white space is reduced. Eventually, the curves will cover all the points “filling” the space.
Now, the question is, if the curve has dimension 1, and it can fill a space in two dimensions, what is the dimension of the space-filling curve?
Fractal Geometry
In 1919, mathematicians Felix Hausdorf, and A.S. Besicovitch answered this problem. A space-filling curve has dimensions between 1 and 2. The dimension approaches 2 as the scale becomes finer and finer (remember the concept of limits?).
The problem above is one of the precursors to the invention of a beautiful type of Geometry now known as Fractals. A fractal refers to objects with fractional dimensions, just like the space-filling curve above. Modern mathematicians realized that our world is too complex to be solely described by one, two, or three dimensions (lines, squares, and spheres). We need have fractional or fractal dimensions
If you noticed, the curves above are self similar. This is one of the characteristics of many fractals. The fractal called Koch’s snowflakes for instance, can be constructed by dividing the sides into three and forming some sort of equilateral triangle.
Of course, there are more complicated fractals and there are amazing ones too. The preceding fractal, for example, models a mountain.
To be concluded.
_____
All images above are from Wikipedia. You can go to the original file by clicking the images.