Mathematics: The Science of Patterns
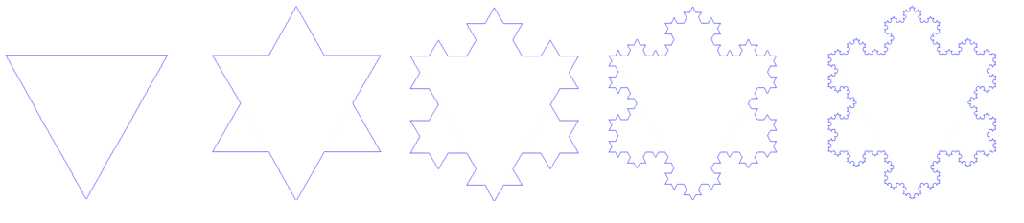
Since elementary grades, we have learned that mathematics is closely related to patterns. Given a sequence of numbers, we would know the next few terms without much effort. We know that the next three terms in the sequence 3, 7, 11, 15, are 19, 23, and 27. Just by looking at the Koch’s snowflake shown in the first figure, we have an idea of how to draw the sixth figure. It may not be as accurate as a computer drawing, but we would surely be able to draw the necessary details. These patterns are obvious and intuitive, so it is easy to predict the next “terms.”
A little more challenging pattern is shown the second figure. Observing the colors of the circles, we can see that the sum of the first odd integers is
, the sum of the first
odd integers is
, the sum of the first
odd numbers is
, and so on. From the pattern, we are quite confident that the sum of the first
odd integers is
without having to exhaust the 999 odd integers.

In general, we can say that the sum of the first odd integers is equal to
. Although this can be proven by mathematical induction, we have an idea that this is true for all cases by looking at its geometric representation.
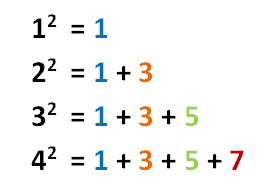
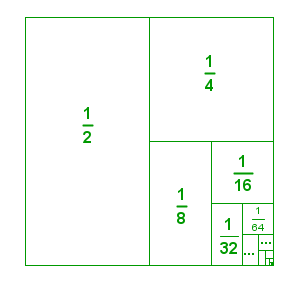
There are also patterns in mathematics that are counterintuitive. For example, if we get the sum of
(where the symbol means “and so on;” that is, we add all the following fractions based on the pattern), intuition tells us that we have infinitely many fractions, so it is impossible to get the exact sum. The geometric representation of this problem as shown below, however, proves that statement wrong. After dividing a square of area
into two, we have two
s. Dividing the other half by
, we have one
and two
s. Dividing the other fourth by
, we have one
, one
, and two
s. Notice that if we continue this process, we will just be dividing the parts of the square, so the total area will not change. Therefore, the sum of all the fractions above equals
.
 Our ability to recognize and generalize patterns enables us to create models and study a wide variety of real-world phenomena. Through patterns we can predict the weather, we can estimate world population 20 years from now, know the probability of a smoker to get cancer at age 60, and so on. Through patterns, we can expedite progress. Through patterns, we can avoid disasters. Through patterns, we can save lives.
Our ability to recognize and generalize patterns enables us to create models and study a wide variety of real-world phenomena. Through patterns we can predict the weather, we can estimate world population 20 years from now, know the probability of a smoker to get cancer at age 60, and so on. Through patterns, we can expedite progress. Through patterns, we can avoid disasters. Through patterns, we can save lives.