Tag: proof by mathematical induction

Mathematics: The Science of Patterns

General Education, High School Mathematics

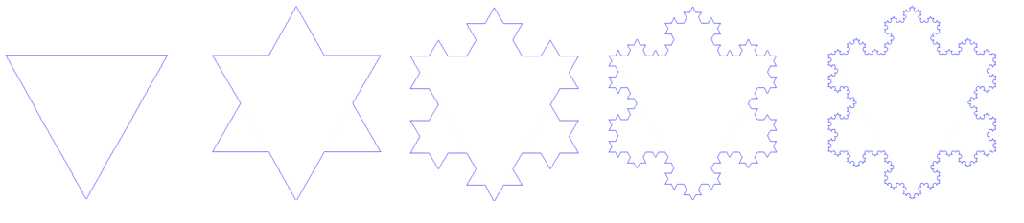
Since elementary grades, we have learned that mathematics is closely related to patterns. Given a sequence of numbers, we would know the next few terms without much effort. We know that the next three terms in the sequence 3, 7, 11, 15, are 19, 23, and 27. Just by looking at the Koch’s  snowflake shown in the first figure, we have an idea of how to draw the sixth figure. It may not be as accurate as a computer drawing, but we would surely be able to draw the necessary details. These patterns are obvious and intuitive, so it is easy to predict the next “terms.”

koch-snowflake1

A little more challenging pattern is shown the second figure. Observing the colors of the circles, we can see that the sum of the first 2 odd integers is 2^2, the sum of the first 3 odd integers is 3^2, the sum of the first 4 odd numbers is 4^2, and so on.  From the pattern, we are quite confident that the sum of the first 1000 odd integers is 1000^2 without having to exhaust the 999 odd integers. » Read more

Leave a comment , , , ,

Dominoes and Mathematical Induction

College Mathematics, Number Theory

Dominoes are Falling Down

If you queued ten thousand dominoes on a very long table and you want to let them all fall just by letting the first domino fall, then how would you queue it?

The best idea probably is to queue them such that:

  1. When the first domino falls, it will hit the second domino.
  2. Make sure that each domino will hit the domino next to it and that each hit domino will fall.
  3. If conditions (1) and (2) are satisfied, then all the dominoes will fall.

The domino effect

In fact, no matter how many dominoes we put on the table, as long as conditions (1) and (2) are satisfied we are sure that all the dominoes will fall. » Read more

11 comments , , , , ,