The 0.0001 Time Rate Approach
by Armand Gelig Macapagong
I encountered Differential Calculus when I was in my 2nd-year High School. As a part of the Math Magi, a Mathematics club in our school, we were taught advance topics apart from our daily Math subjects in class. One of these was an introduction to Differential Calculus. I found Differential Calculus as one of the interesting subjects and my favorite topics were L’Hospital’s rule and Maxima-Minima.
When I went to college, I encountered Differential Calculus again. This time, it becomes a lot easier since I already had a taste of this subject. But what caught my attention was that, a lot of students in our class failed in almost all quizzes. This brought me to thinking, that if I can introduce an easier concept to my classmates, or if I can develop a less complex approach which they can easily grasp, maybe I can help them. So I worked hard in finding an easier approach. I developed this technique two years after that Differential Calculus subject. So, I never really had the chance to help my classmates back then.
This technique eliminates the need of lengthy differentiating while arriving to almost exact answers in solving time rates.
Say for example, we solve this very basic problem:
A balloon leaves the ground 18 m from an observer and rises vertically at 1.25 m/s. How fast in m/s is the balloon receding from the observer after 8 seconds?
Solution: The usual Differentiation approach would be this
By using Pythagorean Theorem, we get
(eq. 1)
when m
m
Differentiating eq. 1, we get
m/s.
But I have a more basic concept than this and when you learn to master this, you can just use your calculator directly without any need for pen and paper.
The 0.0001 Time Rate Approach
denotes the differential change in distance over the differential change in time. Differential change means a very minute or unnoticeable change. We can have this change as 0.0001. This value is the most realizable value for the change in time.
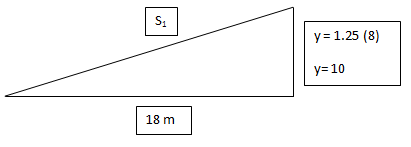
First, we have to consider the initial condition of the problem, or let us call it Frame 1.
Motion films consist of different frames to produce seeming movement of the characters. We will now use this concept in solving the problem, where frame 1 and frame 2 are the frames in the span of the differential change in time.
The first frame would involve the initial condition wherein t=8 seconds, thus;
Solving for , we have
m. I would advise you not to round off any value when using the formula, in order to maintain the accuracy of the value desired value. You can just store the values into your calculators.
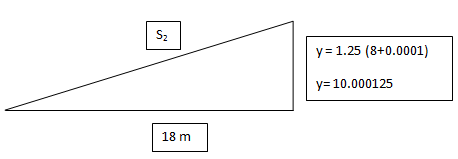
Next, we consider the second differential frame with a change in time of seconds. We will let the balloon rise for
seconds which is a very unnoticeable change in y, thus;
Solving for , we have
m
Since we are looking for $latex we want the speed of the balloon relative to the eyes of the observer. We know that . Since we have all values, we are ready to substitute.
,
(Correct!)
We have arrived to the same answer!
Once you mastered this technique, you will learn to solve this type of problem this way;
V = 0.607056563 m/s
Amazing isn’t it? This technique is applicable in almost all problems in Differential Calculus involving time rates.
But you have to fully grasp the concept first before trying this one. Moreover, before you adopt this technique, you should master Differential Calculus first. It’s always better to learn the hard way around. It’s more fulfilling.
Stay tuned for more topics in Differential Calculus. To God be the glory!
About the Author
Armand Gelig Macapagong is a Civil Engineering student of University of Cebu. He spends his free time solving Math problems and discovering easier approaches on harder Math topics