The Mathematics of Perspective Drawing

Painters use different techniques to create realistic paintings. Vincent Van Gogh’s Flower Beds in Holland is one of the examples of such.  Given the right distance, you would mistake it for a faded photograph.

But how do painters put so much life in their works? How do they put real space (3 dimensions) on a flat surface (2 dimension)?

One of the techniques used by painters is called perspective.   Perspective is the art of drawing objects in such a way so as to give them depth and show their distance from the observer. This gives a drawing the illusion  of three-dimensional space.

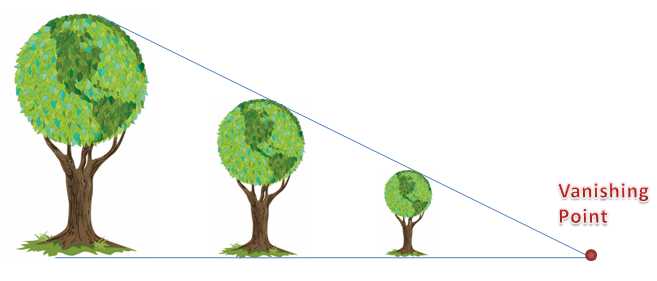
In one-point perspective, the drawings guided by the geometry of converging lines.  The lines meet at a point called the vanishing point as shown in the second figure. Van Gogh used this technique in the painting above.

The mathematics of perspective drawing lies on the ratios of objects drawn. In one-point perspective, objects are proportional (read Introduction to Similarity for a detailed mathematical explanation).  It means, as shown below, that the quotient , where is the height of the tree and is the distance from the vanishing point is always the same. That is, if we make the following representations

: height of the “tallest tree” in the drawing
: distance of the “tallest t tree” from the vanishing point
: height of the middle tree in the drawing
: distance of the middle tree from the vanishing point
: height of the “shortest tree” in the drawing
: distance of the “smallest tree” from the vanishing point

then

.

Note that I placed the quotes on largest tree and shortest tree because if the trees were real, they would have the same height.

 

One-point perspective is just one of the many techniques in perspective drawing. There are also two-point perspective, three-point perspective, and atmospheric perspective. The combination of these techniques creates realistic and life-like drawings.