Semiregular Tessellations: Adventurous Ideas for Floor Tiling

If you are planning to tile your your floor and want something different from the usual tiling which is usually made up of rectangles or squares, the following semiregular tessellations might give you some ideas.

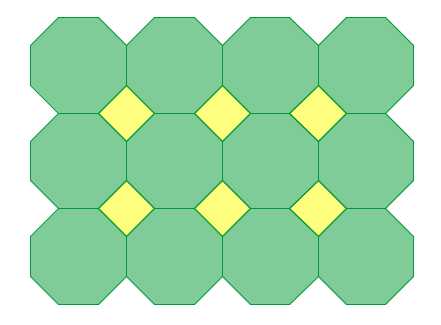
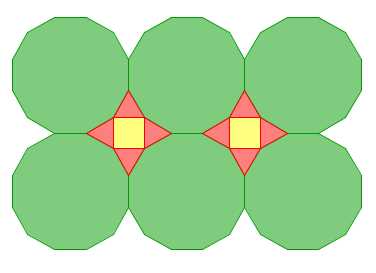
In the first figure, the tessellation is made up of squares and octagons (8-sided polygons).

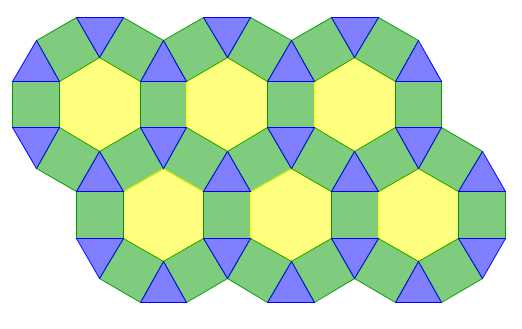
The second figure is made up of squares, equilateral triangles, and hexagons (6-sided polygons).

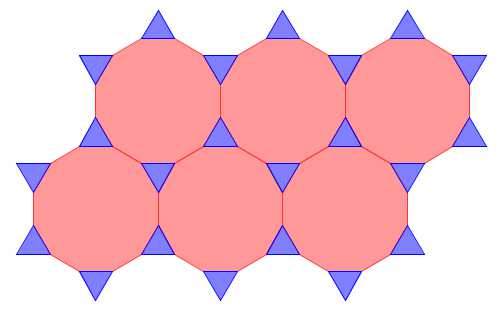
The third figure is made of equilateral triangles and dodecagons (12-sided polygons).

In the fourth figure, the tessellation is composed of squares and equilateral triangles.

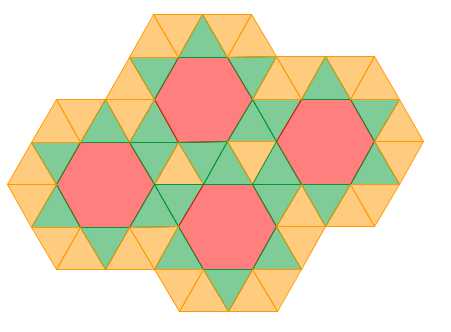
In the fifth figure, the tiling is composed of hexagons (6-sided polygons) and equilateral triangles.

In the sixth figure, the tiling is made up of dodegacons (12-sided polygons), squares, and equilateral triangles.

The tessellations above do not only display beautiful patterns. Mathematical considerations are needed to create such tessellations. For instance, in the last figure, there are points where the vertices of a a dodecagon, a square, and two equilateral triangles meet. The interior angles of these polygons measure 150, 90, 120 degrees respectively. Observe that the angle measures add up to 360 degrees. Only combinations of polygons whose interior angles add up to 360 degrees will tessellate without gaps or overlaps (Can you see why?).

Note: All the tessellations above were created using GeoGebra.