Paper Folding: How to Construct an Equiangular Triangle
Paper folding or origami can be used to create intricate and stunning designs. In addition, paper folding can also be used to teach or learn mathematics. In this post, we use a square piece of paper to construct an equiangular triangle. After the construction, we prove that the triangle is equiangular.
Steps in Constructing an Equiangular Triangle
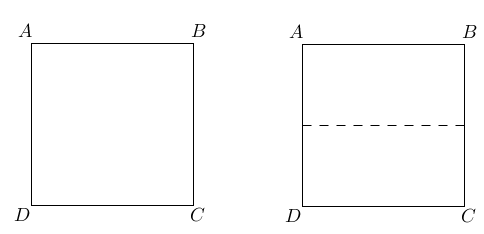
1. Cut a square piece of paper. For the sake of discussion, we label the square ABCD.
2. Fold at the center so that AB coincides with CD . Crease well, then unfold.
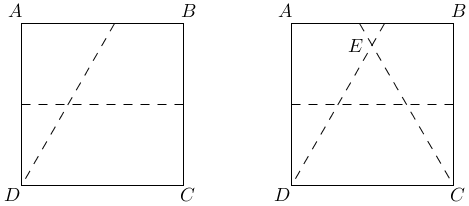
3. Select vertex and fold so that A falls on the center line and the crease passes through D. Unfold.
4. Select vertex and fold so that B falls on the center line and that the crease passes through C. Unfold.
5. Let E be the intersection of the crease formed in steps 3 and 4. Triangle DEC is an equiangular triangle.
In the next section, we discuss the mathematical proof why DEC is an equiangular triangle.
The Mathematical Proof
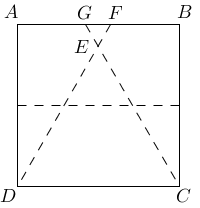
Let F be the intersection of AB and the crease passing through D and let G be the intersection of AB and the crease passing through C.
Now, FD is twice FA (why?), so triangle DAF is 30◦-60◦-90◦ triangle. This means that angle ADF, the angle opposite the shorter side of the triangle measures 30◦. This means that angle EDC = 60◦.
Also, triangle CBG is a 30◦-60◦-90◦ triangle which implies that angle DCE = 60◦.
Therefore, by the Angle Sum Theorem, angle DEF = 60◦.
So, triangle DEF is an equiangular triangle.
Reference: Paper Folding: Art and Mathematics (A local book). A copy of the book can be bought from the UP NISMED Bookstore. A more detailed presentation of the paper folding can also be found in our Agimat website.