Solving Number Problems Using Model Method
This is the second part of the Word Problem Solving Series on Numbers. In the previous post, I have shown you ways on how to solve number problems mentally by working backward. In this post, I am going to teach you how to use models, rectangles in particular, to solve the problems in the previous post. This representation is called the model method. The model method is very popular in Singapore.
Example 1
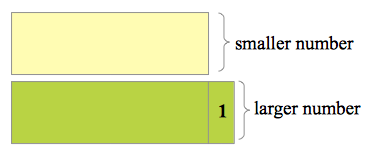
One number is 1 more than the other. Their sum is 47. What are the numbers? Solution
Let us represent numbers using rectangles. The first rectangle is the smaller number, and the second rectangle is the larger which is 1 more than the smaller. Clearly, if take away 1 from the larger number, the two numbers will be equal.
In addition, if we take away 1 from the larger number, then, we also have to take away 1 from the sum which gives us 46 after subtraction. Since the two rectangles have the same size, they will have to split 46 equally. This gives each large rectangle 23 each. This means that the smaller number is 23 and the larger number is 23 + 1 = 24.
Example 2
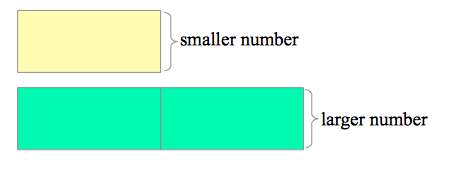
One number is twice the other number. Their sum is 45. What are the numbers? Solution
In this example, the second number is twice the first number. Notice that in this example, if the size of the second rectangle is twice than that of the first rectangle.
This means that you can distribute the sum to the three rectangles equally. That is, each rectangle takes 15. So, the smaller number is 15 and the larger number is 30.
Example 3
The sum of two odd consecutive numbers is 64. What is the larger number?
Solution 3
This example is very similar to Example 1. As we have learned in the previous post, the difference of consecutive odd numbers is 2, so the larger number is 2 more than the smaller number. This means that if we subtract 2 from the larger number, the the two numbers will be equal. Again, if we subtract 2 from the larger number, we also subtract it from the sum which makes the sum 62 after subtraction. 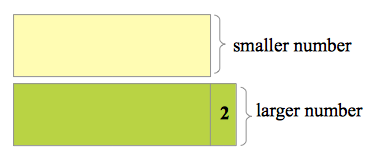 Now, two remaining rectangles with the same size will have to divide the 62, each of which, will get 31. Therefore, the smaller number is 31 and the larger number is 31 + 2 = 33.
Now, two remaining rectangles with the same size will have to divide the 62, each of which, will get 31. Therefore, the smaller number is 31 and the larger number is 31 + 2 = 33.
As you can see, the model method is very good in visualizing simple number problems. Sometimes, you will be surprised that it is also a good way to construct your own problem.
In the next part of this series, we will discuss about using Algebra to solve similar problems.