Solving Math Word Problems in Numbers Using Algebra

This is the third part of the Solving Math Word Problem Solving Series on Numbers for Grade 6 – 8 students. The first part was on solving number problems mentally by working backward. The second part discussed on solving number problems using the model method. In this post, we are going to discuss how to solve word problems using Algebra if the mental and model methods fail. We will start with simple problems and will continue to solve more complicated problems later. We will use the problems we discussed in the first two parts of this series. Note that the discussion in this post is quite detailed because it is designed for beginners particularly middle school and high school students.

Example 1 One number is 1 more than the other. Their sum is 47. What are the numbers?

Solution

First Sentence: One number is 1 more than the other.

If there are two numbers and the other one is 1 bigger than the number, then if the smaller number is 5, the other is 5 + 1 or 6. So, since we don’t know what the number is, we let the number n. This means that the larger number is n + 1. 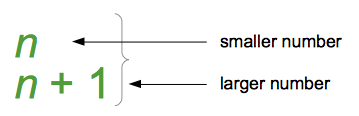 Second Sentence: Their sum is 47.

If you think that the word sum has something to do with addition, you are right. Since their sum is 47. If we place this in a sentence, we say that the sum of n and n + 1 is 47 or the sum of n and n + 1 equals 47. What is the number? This simply means that n + (n + 1) = 47. Solving for n, we have 2n + 1 = 47. This means that n = 23.

Example 2

One number is twice the other number. Their sum is 45. What are the numbers?

Solution First Sentence: One number is twice the other number. 

What is a number and twice its value. Say, the number is 12. What is twice its value? Yes, 24 that is. So, if 12 is one number, the other is twice its value or twice 12 or 2(12) which is equal to 24. Now, if we let n be the number, the other number is 2 times n or 2n. Second Sentence: Their sum is 45. Well, this is just like in Example 1. We add n and 2n and their sum is 45. What is the number? Solving the equation, we have n + 2n = 45,  3n = 45 which results to n = 15.

Example 3

The sum of two odd consecutive numbers is 64. What is the larger number?

Solution

First Sentence: The sum of two odd consecutive numbers is 64.

Seven is an odd number and the next odd number is 9. Seven and 9 are consecutive numbers. Also, 35, 37, and 39 are three consecutive numbers. It is clear that if n is odd number, the next number is n + 2. So, the two consecutive odd numbers whose sum is 64 is n and n + 2.

Two and 3 are consecutive numbers as well as 15 and 16. So clearly, is 15 is a number, 15 + 1 is the next number. Therefore, if n is the smaller number, n + 1 is the larger. What is the larger number? From the discussion above, you should know that the equation is n + n + 2 = 64. This gives us 2n + 2 = 64, 2n = 62 and n = 31 which is the smaller number. The larger number is 31 + 2 = 33. In the next part of this series, we will discuss more complicated number problems.