Domain and Range 1: Basic Concepts

March 4, 2014 GB High School Algebra, High School Mathematics

Domain and range are concepts that are essential in learning functions. In most resources, these concepts are just defined technically, and although there are examples, many just lack intuitive explanations. In this post, we discuss domain and range in a simple and hopefully easy to understand manner.

Example 1: $f(x) = 2x + 1$

Domain

What is the domain of $f(x) = 2x + 1$ and what is its range? Well, the domain are just the possible values of $x$ that will produce a “valid” value $f(x)$ . To check, we can ask the following questions.

Can we substitute positive values to $x$ ?
Can we substitute negative values to $x$ ?
Can we substitute 0 to $x$ ?

Obviously, the answer to these questions are all yes. In fact, we can assign any real number value to $x$ and we can always get a corresponding value for $f(x)$ .

Range

The possible values that you can substitute to $x$ which will result to a valid output is called the domain of the function. The range of the function are all the possible outputs. In this case, we can input any real number as $x$ , and all real numbers can be the possible outputs. Note that we are sure about this because we can pick any $f(x)$ and we can always solve for $x$ . Try $f(x) = 4$ .

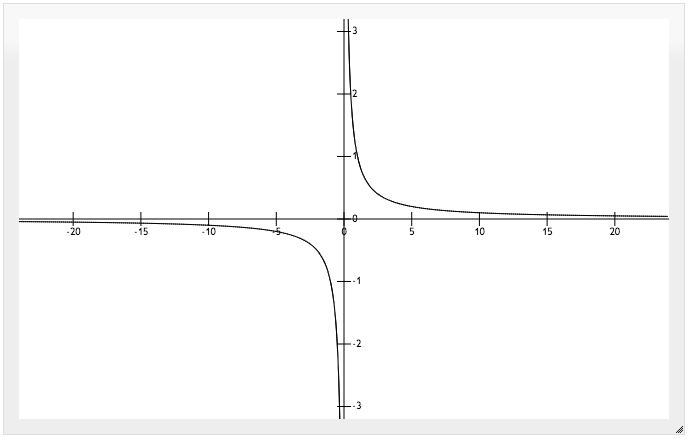
Example 2: $g(x) = \frac{1}{x}$

Domain

In this example, we can substitute any value to $x$ , negative or positive, except $0$ . If we let $x = 0$ , then $g(0) = \frac{1}{0}$ and we know that this is undefined. Therefore, the domain of $g(x)$ is the set of real numbers except $0$ .

Range

If $x$ is positive, then the value of $\frac{1}{x}$ is positive. If $x$ is negative, then the value of $\frac{1}{x}$ is negative. So, $g(x)$ can be both positive and negative. How about $0$ ? Can $g(x)$ be $0$ ? Can you think of any number that we can substitute to $x$ so that $\frac{1}{x}$ is $0$ ? No, the only possible from a fraction to be $0$ is for its numerator to be $0$ ! So, the range is the set of real numbers except $0$ .

Example 3: $h(x) = 2^x$

Domain

In this example, again, we can can substitute any value to $x$ . Can we raise $2$ to any positive number? Yes. Can we raise 2 to 0? Yes. Can we raise 2 to a negative number? Yes.

Here are a few examples:

$2^5 = 32$

$2^0 = 1$

$2^{-3} = \displaystyle \frac{1}{8}$

Since we can substitute any value to $x$ , then we say that the domain of $h(x)$ is the set of real numbers.

Range

As we can observe above, if we substitute a large positive value for $x$ , the value of $h(x)$ becomes large positive numbers. If we substitute $0$ to $x$ , then $h(x)$ becomes $1$ . However, what is interesting is even if we substitute a negative value to $x$ , although $h(x)$ is small, it is still positive. For example, letting $x = -3$ , gives us $\frac{1}{8}$ . If we let $x = -10$ , then $h(x) =\frac{1}{1024}$ which is close to $0$ . In fact, if $x$ is negative, the function becomes

$h(x) = \frac{1}{2^x}$ which is always positive ( and with $x$ also positive).

In addition, as $x$ becomes smaller in the original equation, say -1000, $2^x$ becomes very close to $0$ , it seems safe to say that the value range of $2^x$ is the set of real greater than $0$ .

Now, why not include $0$ ? Because a positive number $2$ raised to any real number exponent is always positive. Therefore, the range of $h(x)$ is the set of positive real numbers.

In the next post, we are going to learn the relationship between the domain and the range and the graph of the function. Please stay posted.

4 comments domain and range, domain of a function, finding the domain and range, functions, how to find the domain and range of a function, range of a function

Domain and Range 1: Basic Concepts

Leave a ReplyCancel reply