One to One Correspondence and Hilbert’s Grand Hotel
In the Understanding Hilbert’s Grand Hotel, we have discussed the brilliant schemes of a hotel manager in accommodating finite and infinite number of guests in a hotel with infinite number of rooms, where each room was occupied by one guest. In other words, the hotel was fully occupied. In this post, I will explain the mathematics behind these schemes. To be able to understand the explanation, it his highly recommended that you read first the post in the link above.
Finite Number Of Guests
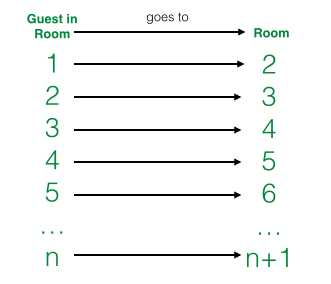
In the Grand Hotel problem, during the first night, a guest arrived. The hotel was full, so there was no room available. However, to accommodate the new guest, the manager requested the guest in Room 1 to move to Room 2, the guest in Room 2 to move to Room 3, the guest in Room 3 to move to room 4 and so on. This means that each guest had to move to the room whose number is 1 higher than the the current room number. This leaves the Room 1 vacant.
Now, how is this possible?
First, if you think of any room number, there is always a room next to it — just add 1. That room exists since there are infinitely many of them. This assures that every guest has a room to move to.
Secondly, since each guest moves to the next room, this assures that no guest will share the same room.
Note that this scheme worked for the 60 guests in the second night, and will always work for any finite number of guests.
Infinite Number of Guests
During the third night, a bus infinitely long arrived containing infinite number of passengers. Again, the hotel was full and each room was occupied by 1 person. The bus needed 1 room for every passenger.
To accommodate the infinite number of guests, the manager asked all guests to move to the room where the number is twice the guests’ current room number. So, the guest in Room 1 moved to Room 2, the guest in Room 2 moved to Room 4, Guest in Room 3 moved to room 6, and so on. Now, what happened after everyone moved? All the odd-numbered rooms were vacant! Now, the passengers in the bus occupied the rooms with odd numbers as shown below.

Now, what does this show?
It shows that the number of counting numbers (1, 2, 3, 4, 5, … ) is equal to the number of even numbers (2, 4, 6, 8, 10, 12,…). This is quite counterintuitive because it seems that the number of counting numbers is twice the number of even numbers. For instance, there are only 5 even numbers from 1 to 10, while there are 10 counting numbers from 1 through 10. This is discussed in the following section.
Understanding One to One Correspondence
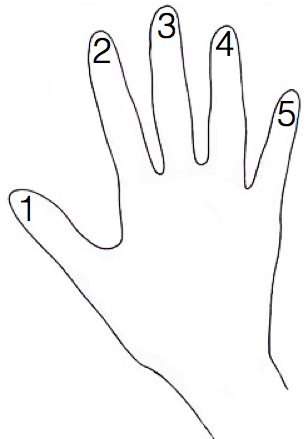
When we count objects, we are pairing the counting numbers with each of these objects. For example, if we count our fingers on one hand, we can assign the numbers as shown below. Of course, we can assign any number to whichever finger we like, as long as one finger is paired with exactly one number. This pairing will result to 5 as the largest number and we say that we have 5 fingers. This one to one pairing is called one to one correspondence.
With one to one correspondence, we can always see if two sets are equivalent (have the same number elements) by pairing one object to another in one-to-one correspondence. We can see that the set with elements {x, y, z} and the set with {a,b,c} are equivalent because we can assign one element in one set to pair with one and only one element in the other set. In effect, if we know that two sets are equivalent, we can count one set and we will know the number of elements of the other set. For example, in a dance contest where participants are paired composed of a man and a woman, then, we don’t really need to count all the participants if we want to know the total number of participants. We can just count the number of men (or women) and we will know how many participants are there.
One to One Correspondence in Infinite Sets
The one to one correspondence in finite sets can be extended to infinite sets. If we can pair two sets in a way such that no element is left out, then we know that these two sets have the same number of elements. This is shown the second diagram above, where each number is paired with an even number. The pair of 1 is 2, the pair of 2 is 4, the pair of 3 is 6 and so on. Given any n, there is exactly one and only one pair which is 2n. Therefore, the number of counting numbers and the number of even numbers is the same. They have the same number of elements.
As I have mentioned above, if we can pair two sets such that we are sure that nothing is left out, then, we are sure that the two sets have the same number of elements. In the diagram above, notice how I paired the number of counting numbers and the number of integers including 0, positive, and negative. The alternating method assures that no integer is left out without a pair, no matter how further we go. This shows that the number of counting numbers is equal to the number of integers. You might also be surprised that there are as many factions as counting numbers (I will discuss this later).
Final Note
The concept of infinite sets was formalized by German mathematician Georg Cantor. During his lifetime, his theories was rejected by many top mathematicians. It was only in later years that modern mathematicians were able to grasp the brilliance of Cantor’s work.