An Explanation Why the Line Multiplication Trick Works
Mathematical concepts and operations can be represented in different ways. For example, a function can be represented using a table, set of ordered pairs, equations, or graphs. Another example is an equation which can also be represented as a balance.
In this post, we are going to discuss a representation of a simple concept which is very popular among netizens: multiplication of numbers using lines. Many are amazed about this representation that they even call it the magic line multiplication trick.
Note: If you don’t know the trick, watch first the video below.
Now, let us learn why the line multiplication trick works.
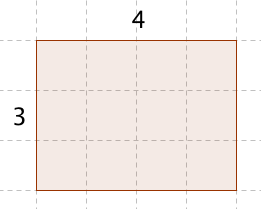
Multiplying 2-digit numbers can be represented geometrically as area. The multiplication 4 × 3, for example, can be represented as a rectangle with length 4 and width 3 as shown above. The product which is equal to 12 is the area of the rectangle.
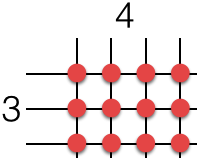
Notice that if we actually draw the squares (see dashed lines above), we have 4 as the number of columns and 3 as the number of rows. This representation is the same as drawing vertical 4 vertical lines and 3 horizontal lines, and this time the product is the number of intersections.
In the representation, the lines serve as the number of columns and rows and the intersections (red circles) “represent” the squares.
Multiplying 2-Digit Numbers
If we are going to represent multiplication of 2-digit numbers using the representations above, then we can make the following strategy. Since we are multiplying different digits, we will have different rectangles with various areas. But how many? Let us look at multiplying 23 and 12.
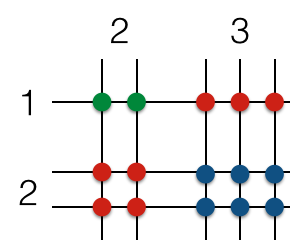
It turned out that we can just arrange the numbers as shown above. The number 23 is represented on the column as 2 columns and 3 columns with space in between. The number 12 is represented by 1 row and 2 rows with space in between. The rectangles are the product of the numbers just like in the first figure. Can you make sense of the figure?
Let us see the connection between the multiplication algorithm and the figure. When we multiply 2-digit by 2-digit numbers, we do the following.
(1) Blue rectangle: get the product of the ones digit of both the multiplicand and the multiplier;
(2) Red rectangles: get the product of the ones digit of the multiplicand and tens digit of the multiplier, get product of the tens digit of the multiplicand and the ones digit of the multiplier, and then add them;
(3) Green rectangle: get the product of the tens digit of both the multiplicand and the multiplier.
Though I did not mention carrying over, it should be done whenever necessary.
Now, notice that we can make an equivalent representation using lines as shown in the next figure. Here, the numbers are represented by the lines and the products are represented by the intersections (colored circles).
In the preceding representation, the number of blue circles is the ones digit of the product of 23 and 12, the number of red circles is the tens digit, and the number of green circles is the hundreds digit.This process can further be extended to 3-digits or more. That is the reason why the line multiplication trick works.
Watch the video below to learn more about the line multiplication trick.
Enjoy learning and share this post to your friends.