What exactly is the vertical line test?
A function as we have discussed is a relationship between two sets, where each element in the first set has exactly one corresponding element in the second set. If we think of candies which cost 10 cents each, then we can say that 1 candy costs 10 cents, 2 candies cost 20 cents, 3 candies cost 30 cents, and so on. We can think of this relationship as a function since for each number of candies, there is only one possible price.
If we consider the relation y = 2x, then we can say that it is a function since for every value we substitute to x, there is one and only one corresponding value for y. For instance, if x = -3, then y = -6 and and if x = 9, then y = 18 (one y for each x).

The relation h(x) = 8 is also a function because for any value of x, there is one and only one h(x), which in this case equal to 8.
The relation x = y2, on the other hand, is NOT a function since for some value of x there are two possible values for y, positive and negative. For example, for x = 4, there are two possible values for y, that is, 2 and -2.
Graphs of Functions
We can represent functions using graphs. Now, what do we mean that for every value in x in the domain of the function, there is exactly one and only corresponding value for y?
Suppose we have a graph. If we choose any point on the x-axis and draw a vertical line passing through that point, the intersection of the vertical line and the graph of the function is (x,f(x)).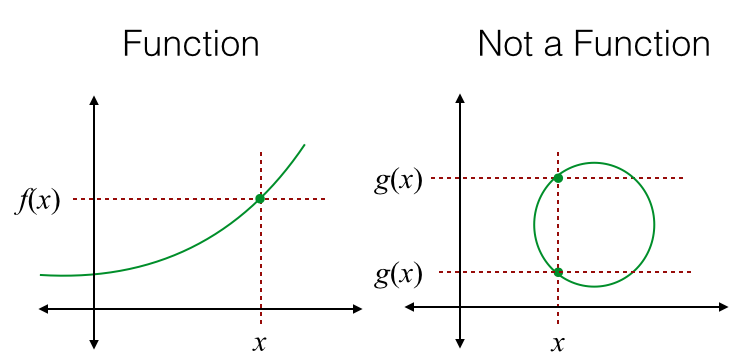
Observe the two graphs above. In the definition, for any x, there is one and only one corresponding value of y. Graphically, for any x means any line with equation x = a which is graphed as a vertical line in the Cartesian plane. The phrase there is only one corresponding value of y means that the line x = a must only intersect the graph at most one time. In the first graph, in the relation f, for every x;that we choose (we can choose any point on the x-axis under the graph), we see that if we draw a vertical line, it will only intersect the graph once. This means that there is only one y value which is f(x).
On the other hand, in the second graph, in the relation g, if we chose any value x value, then there are two values for g(x). This violates the definition of a function. . Of course, if we can find only one value for x that has two or more y values, then we are sure that the relation is not a function.
The discussion is the same as if a vertical line hits two points on a graph, then, the graph is not a function. That is why we call it the vertical line test.
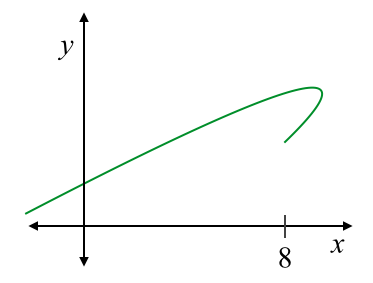
Exercise: Consider the graph below. Is it a function or not? Explain why.
Answer: Although you a vertical line will intersect the graph once until x = 8, after 8, a vertical line will intersect the graph twice. Therefore, it is not a function.