A Closer Look at Coinciding Lines
In the previous post, we have asked a question about coinciding lines. We observed that the lines with equations and
coincide. It is not difficult to see that
is
. The question now is if one equation is a multiple of the other, are their graphs coinciding? We answer this question below.
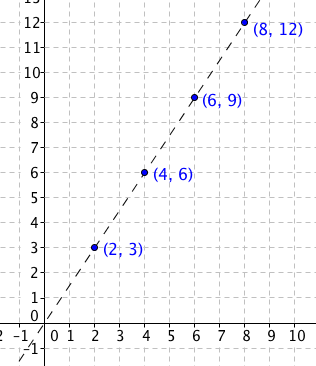
Consider a point with coordinates (2,3). What happens if we multiply the coordinates by 2, 3, and 4? If we do this, the coordinates become (4, 6), (6,9), and (8,12). Now, what is so special about these points? As we can see in the graph below, they lie on the same line. Can you explain why?
If we create a point in (0,0) and connect it to (2,3) with a segment, then the segment has slope 3/2. If we connect the other points to (0,0) their slope will be 6/4, 9/6, and 12/8, all of which are equal to 3/2. Since they have a common point which is the origin, and have the same slope, they lie on the same line (recall slope-intercept form).
This can be generalized as point not on the origin with coordinates . This point has slope
. Now, if we multiply the coordinates with any real number
which is not equal to 0, then the coordinates become
. The slope of the segment connecting this point and the origin is
which is still equal to
.
Now, since multiplying an equation with a number is just like multiplying all the coordinates of the points by this number, therefore, all those points are still on the line. This is the reason why the lines are also coinciding.