What is the horizontal line test?
In January of this year, we have discussed about the vertical line test. We have learned that if a vertical line intersect a graph more than once, then that graph is not a function. In this post, we learn about the horizontal line test and its relation to inverse functions.
Suppose we have a function . Then, we input
and call the output
. If we do things backward, suppose we have the number
which is in the range of
. What value should we input to
to get
? Let’s have a more specific example.
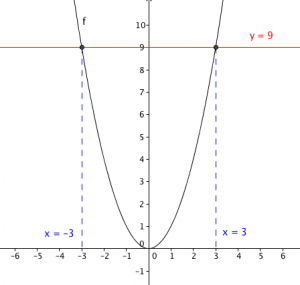
Suppose we have the function . And we choose the number
which is in the range of
. What number should we input in
to get
? Well, we will have two numbers, those are
and
.
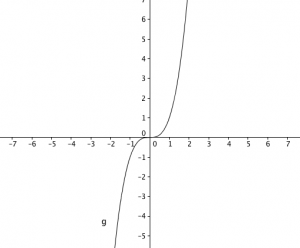
On the other hand, suppose we have the function . And we choose the number
. What number should we input in
to get
? We only have one and only one number which is equal to
. Now this is true for any
in
since there is only one cube root of any number.
Now if there is one and only one value of which satisfies
for each
, then we can define a new function which reverses the transformation. Given the output
, there is one and only one input
that results to
. This function is called the inverse function.
Notice from the graph of below the representation of the values of
. Graphically,
is a horizontal line, and the inputs
and
are the values
at the intersection of the graph and the horizontal line. In fact, if you put a horizontal line at any part of the graph except at
, there are always 2 intersections. As we have learned in functions, for every input, there is exactly one output and hence reversing
will have two outputs. Thus, it cannot qualify as a function and therefore it has no inverse function.
However, if we examine the graph of , a horizontal line can only intersect it at one point regardless of where you place it. Therefore,
has an inverse function.
From the discussion above, we can conclude that we can use horizontal lines to test whether a function has an inverse or none. That is, if every horizontal line intersects the function at most once, then the function has an inverse; otherwise, it has no inverse function. This method is called the horizontal line test.