Proof Without Words: If x >0, x + 1/x >=2
A picture is worth a thousand words, even in mathematics. Sometimes, complicated algebraic expressions can be shown using very simple geometric representations. One example is the sum
which equals 1.

In this post, we show another proof without words. Proof without words is not a proof per se but rather a representation that will help readers understand a proof.
Theorem: If ,
.
We can test a few examples. Since , we can test a few positive integers. Suppose
, then
.
Now,
if ,
Notice that as increases,
increases, so for
,
.
We can also test numbers between 0 and 1. For example, , then
.
Also, for x ,
.
As we can see, they are also greater than 2.
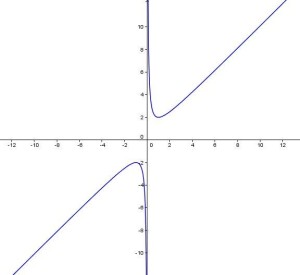
Instead of substituting x by individual values, we can also graph the function . As we can see in the graph below, the condition
represents the area of the Cartesian plane to the right of y-axis.
It is clear that the graph on that area is above the x-axis and all its parts is greater than or equal to 2. But again, this is not the proof since we cannot see all the parts of the graph.
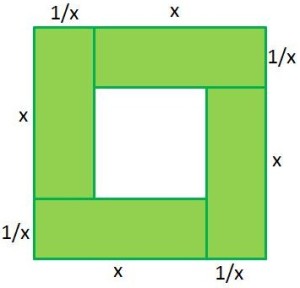
The Proof Without Words
We can form rectangles with dimensions and
. The area of each of these rectangles is equal to
.
The area of the square containing the four rectangles is . This is because it includes the area of the four green rectangles (4 square units) and the area of the white square in the middle. Therefore, getting the square root of both sides of the inequality,
is greater than or equal to 2. Therefore,
.
Adapted Proofs without Words: Exercises in Visual Thinking by Roger B. Nelson