The Basics of Direct Proportion

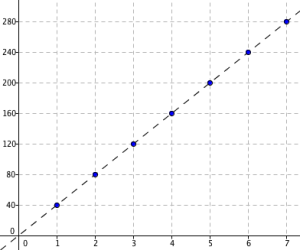
A car travels at 40 kilometers per hour traveled for 7 hours. The table of the distances traveled with respect to time is shown below.

Observe the relationship between the distance traveled and the time. As the time increases, the distance traveled increases. If the number of hours increases two times, then the distance also increases two times. Between hour 1 and hour 2, the increase in time is 1 hour, and the increase in distance is 40 kilometers. Between hour 3 and hour 5, the increase in time is 2 hours, and the increase in distance is 2(40) = 80 kilometers.

If there are two changing quantities and and if the value of changes 2 times, 3 times, and so on, also changes 2 times, 3 times, and so on respectively, we can say that is directly proportional to . In the relationship above, distance is directly proportional to time. 

If there are two changing quantities and and is directly proportional to , then we can use the equation , where is a constant. In the relationship above, if we let be the distance and be the time, the . In the first column, we have t = 1 and d = 40, so

d = kt
40 = k(1)
40 = k

Since k (the constant) is equal to 40, this means that d/t is always equal to 40. Yes, 80/2, 120/3, 160/4, … and so on have quotient 40.

Graphs of direct proportion are linear functions. This can easily be seen because of the constant difference in both and .

From this post we have learned that direct proportion is the relation between quantities whose ratio is constant. In the next post, we are going to learn the basics of inverse proportions.