The Basics of Inverse Proportion
In the previous post, we have discussed the basics of direct proportions. Recall that when two quantities and
change and if
changes n times, then
changes n times, then we can say that
is directly proportional to
. In this post, we are going to learn about inverse proportions.
Problem
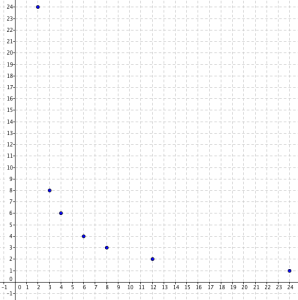
A rectangle has area 24 square units. Find the possible areas if the length and width are both whole numbers.
Solution and Discussion
The table shows the pairs of length and width that has area of 24 square units.
Let us consider the first column as a reference pair. Notice that when the length becomes 2 times (see second column), then the width becomes ½ times (24 becomes 12). When the length becomes 3 times (1 becomes 3), then the width becomes 1/3 times (24 becomes 8). Verify if this is true with the others.
When two quantities and
change, and if
changes 2 times, 3 times 4 times, and so on, and y changes ½ times, 1/3 times, and ¼ times, then we can say that
is inversely proportional to
.
Notice that the area of the rectangle above is constant, so the product of length and width is always constant. Therefore, if is directly proportional to
, then
, where
is a constant. We can also derive the formula
.
As show in the previous post, the graph of a direct proportion lies on a straight line. Notice that the graph of inverse proportion is a curve which is high near the y-axis and approaches the x-axis as x-increases.