The effect of adding b to the linear function y = ax + b

In the previous post, we have learned about the effects of a in the linear function with equation y = ax. In this post, we learn about the effects of adding b to that equation. That is, we want to learn the effects of b in the linear function with equation y = ax + b.

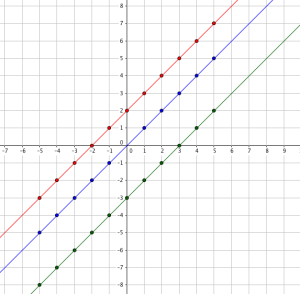
Consider the graph of the functions y = x, y = x + 2 and y = x – 3. The table of values (click figure to enlarge) below shows the corresponding y values of the three linear functions. The effect of adding 2 to the function y = x adds 2 to all the y values of y = x. This implies that in the graph, all the points with corresponding x values are moved 2 units above the graph of y = x. In addition, in the graph of y = x – 3, the -3 subtracts 3 from all the y values of y = x. In effect, all the points  with corresponding x values are moved 3 units below the graph of y = x.

In addition, for y = x, if x = 0, y = 0. That means that the graph passes through the origin. On the other hand, for y = x + 2, when x = 0, then y = 0 + 2 = 2. This means that the graph passes through y = 2. Further, for y = 0 – 3 = -3. This means that the graph passes through y = -3. These are shown both in the table above and in the graph below.

From the observation above, we can see that the graph of the function y = x + b, passes through y = b. This can be easily seen because at x = 0, y = 0 + b which mean that y = b. Further, for the general linear function y = ax + b it has the same effect. If x = 0, then y = a(0) + b = b. Therefore, the graph of y = ax + b, passes through y = b. So, in function y = ax + b, b is the y intercept of the function.