Increasing and Decreasing a in the linear function y = ax

In the previous post, we have learned the effect of the sign of a in the linear function . In this post, we learn the effect of increasing and decreasing the value of a. Since we have already learned that if , the graph is a horizontal line, we will discuss 2 cases in this post: , and .

Case 1: a > 0

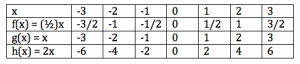
Let us consider several cases of the graph of where . Let the equation of the functions be , , and making , , and , respectively. As we can see from the table, for the same , the larger the slope, the larger its corresponding y-value. This means that for , the point is above and that the point is above . We can say that as increases, is increasing faster than , and is increasing faster than the increase in . 

For the same , the smaller the slope, the smaller its corresponding y-value. That means that for , the point is below and that the point is below . We can say that as decreases, the decrease in is faster than the decrease in , and the decrease in is faster than the decrease in .

Generalization 1: In the function where , the larger the value of the , as increases the faster increases.

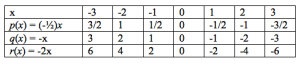
Case 2: a < 0

Letting is just reversing the signs of the y-values making reflecting the graph on the y-axis. This means that the graph is decreasing as $x increases. This means that the graph goes down to the right.

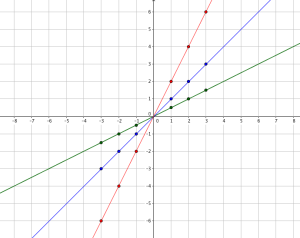
From the table above and from the graph below, we can deduce that the smaller the value of the slope, the function decreases faster. Again, the faster the decrease, the steeper the graph.

Generalization 2: In the function where , the smaller the value of the , as increases the faster decreases.

From the two generalizations above, we can say that in the graph of , as the absolute value of a increases, the larger is the y value and the steeper its the graph.