Note: This is the second part of the the Slope Concept Series. The second and third articles are Part I – Understanding the Basic Concepts of Slope and Part III – Slopes of Vertical and Horizontal Lines.
***
In the Understanding the Basic Concepts of Slope post, we have discussed that slope is described as rise over run. In this post, we are going to show that the slope of a straight line is constant.
To get the slope of a straight line or a segment, we determine two points on the line, say A and B, draw a horizontal line through point A and a vertical segment through point B. We then determine the intersection of the two line segments and name it C as shown in Figure 1. Angle C is a right angle since BC is a vertical segment and AC is a horizontal segment.
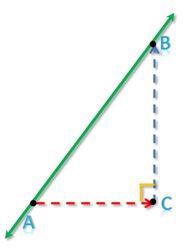
Figure 1 - A line containing points A and B.
The slope of the line containing AB is  . If we determine two more points, say D and E on the line, and do the process mentioned above, we can come up with triangle DEF right angled at F as shown in Figure 2. In terms of DEF, the slope of the line containing points D and E is
. If we determine two more points, say D and E on the line, and do the process mentioned above, we can come up with triangle DEF right angled at F as shown in Figure 2. In terms of DEF, the slope of the line containing points D and E is  . Since the line containing DE and AB is practically the same line, we have learned from high school mathematics that their slopes must be equal. Hence, the following relationship holds:
. Since the line containing DE and AB is practically the same line, we have learned from high school mathematics that their slopes must be equal. Hence, the following relationship holds:  .
.
Why is this so?
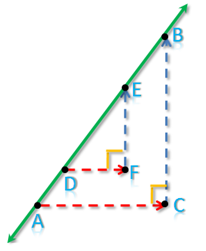
Figure 2 - Triangle ABC and DEF with their hypotenuse contained on the line.
To show that the slope of the line is constant, we must show that  .
.
Proof That the Slope of a Straight Line is Constant
From Figure 2, BC is parallel to EF, since they are both vertical segments. Similarly, DF is parallel to AC, since they are both horizontal segments. By the Parallel Postulate, we can consider AB as a transversal of the two pairs of parallel segments.
We can see that angles DEF and ABC are congruent since they are corresponding angles. Angles C and F are also congruent since they are both right angles. Hence, by AA similarity, ABC is similar to DEF. Since the ratio of the corresponding sides of a similar triangles are equal, it follows that  .
.
From the above proof, we have shown that the slope of a straight line, or the slope of the graph of a linear function, is constant.
. In this post, we learn the effect of increasing and decreasing the value of a. Since we have already learned that if
, the graph is a horizontal line, we will discuss 2 cases in this post:
, and
.
where
. Let the equation of the functions be
,
, and
making
,
, and
, respectively. As we can see from the table, for the same
, the larger the slope, the larger its corresponding y-value. This means that for
, the point
is above
and that the point
is above
. We can say that as
increases,
is increasing faster than
, and
is increasing faster than the increase in
. » Read more