Understanding Line Symmetry

Many people believe that symmetry is beauty. Nature is full of symmetric objects. There are many man-made structures that are also symmetric. In this post, we are going to discuss some of the basic mathematical properties of symmetric objects. We will limit our discussion to line symmetric objects.

Line Symmetry

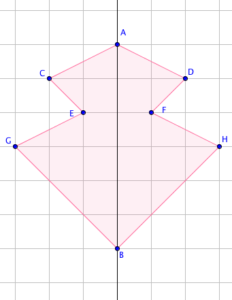
A figure is line symmetrical when it can be folded along a straight line such that the folded shapes fit exactly on top of each other. The fold line is called the line of symmetry.

When a symmetric figure is folded along its line of symmetry, the parts that are on top of each other are called the corresponding parts. In the polygon below with line of symmetry AB, points C and D are corresponding points, segments GB and HB are corresponding sides, and angle G and angle H are corresponding angles. Since the folded shapes fit exactly on top of each other, the corresponding angles are congruent and their corresponding sides are also congruent. 

Exercise:

(1) What is the corresponding point of point G? of segment DF? of angle D?
(2) Identify two pairs of congruent angles and two pairs of congruent sides.

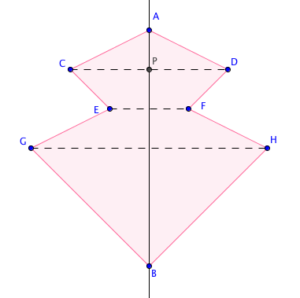
If you connect the corresponding points of a line symmetric figure, the line segment connecting them is perpendicular to the line of symmetry (Can you see why?). This means that their distances from the line of symmetry to the corresponding points are equal. In the figure below, the distance from point P to point C is equal to the distance from point P to point D. That is, .

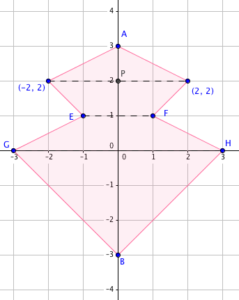
In the coordinate plane, if the line of symmetry is the y-axis, then the corresponding point of (2,2) is (-2,2). Since they are on the same horizontal line, their y-coordinates are equal. In addition, since they are on the opposite sides of the y-axis and equidistant from it, their x-coordinates have the same absolute value but the signs are opposite. For example, if a figure contains a point whose x-coordinate is 3, the x-coordinate of the corresponding point is -3. As we can see |3| = |-3| = 3. From this, we can generalize that if a point (a,b) is a part of a figure whose line of symmetry is the y-axis, then its corresponding point is (-a,b).

Using the same reasoning above, if the line of symmetry is the x-axis, then the points are on the opposite side of the x-axis. This means that the y-coordinates of the corresponding points have opposite signs. That is, corresponding point of the point with coordinates (a,b), is the point with coordinates (a, – b).