Understanding Point Symmetry
In the previous post, we have learned about line symmetry. In this post, we are going to learn about point symmetry, another type of symmetry.
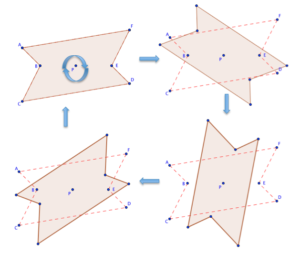
If a figure is rotated 180 degrees about a point and it coincides with its original position, then it is said that the figure has point symmetry. The point of rotation is called the point of symmetry.
The figure below shows the point symmetric polygon ABCDEF rotated clockwise about P, its point of symmetry. The polygon outlined by the dashed line segments shows its original position.
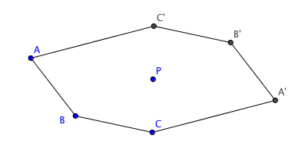
When a point symmetric figure is rotated 180 degrees, then the matching points are called corresponding points. The matching sides are called corresponding sides and the matching angles are called corresponding angles. Clearly, in a point symmetric figure, since the shape is not changed while being rotated, the corresponding sides are congruent and the corresponding angles are also congruent. Therefore, in the figure above, angle A is congruent to angle D since they are corresponding angles, and side EF is congruent to side BC since they are corresponding sides.
In a point symmetric figure, the line connecting the corresponding points always passes through the point of symmetry. Also, the corresponding points are equidistant to the point of symmetry. In other words, every part of the figure has a corresponding part: the same distance from the point of symmetry but in the opposite direction. In addition, the corresponding sides of the figure are parallel. This means that the distance between P and C is equal to the distance between P and F because C and F are corresponding points. Also, side AB is parallel to side DE because they are corresponding sides.
Creating Point Symmetric Figures
With the properties stated above, we can easily create polygons that are point symmetric using the following steps.
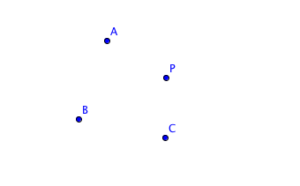
1.) Create a point of symmetry P.
2.) Create points A, B, C, and so on, which are vertices of the point symmetric figure.
3.) Create rays AP, BP, CP and so on which are rays connecting the points and the point of symmetry.
4.) Determine the corresponding points A’, B’, and C’ and so on so that AP = A’P, BP = B’P, CP = C’P and so on.
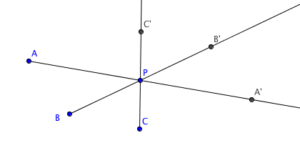
5.) Draw the polygon by connecting the points A, B, C, … , A’, B’, C’ and delete unnecessary objects.
The figure above ABCA’B’C’ is a figure with point symmetry. Point P is the point of symmetry. This means that when the figure is rotated about P, it will coincide with its original position.