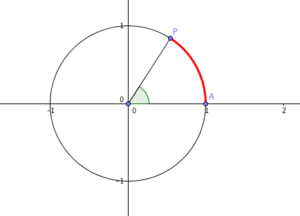
Understanding Radian Measure
A circle O with radius 1 unit has its center placed at the origin. Let A be its intersection with the x-axis at (1,0) and P be another point on its circumference. If we move P along its circumference, then we can determine the distance traveled by P. If we let A be the starting point of P as it moves counterclockwise, then the distance traveled by P is equal to the length of arc AP represented by the red arc in the following figure.
To be able to know the length of arc AP, first, we must know the total distance traveled by P from A going counterclockwise and back to A (i.e. complete revolution). That is, we need to find the circumference of the circle. Since a unit circle has radius 1 unit, its circumference C is
.
We know that as P moves, we can also measure angle AOP in terms of degrees. Now, one complete revolution is equal to 360 degrees. Therefore, degrees and
degrees.
To find the amount of rotation of P in terms of degrees after traveling 1 unit, we have
This gives us the following equations,
.
We know that , so we get
degrees. This means that the position of P where the arc length of AP is equal to 1 is the same as the position of P when it is rotated approximately 57.29 degrees counterclockwise about the center of the circle from A. From here, it is not difficult to observe that for each amount of rotation in degrees, there is also a corresponding arc length. Therefore, we can also consider arc length as a unit for amount of rotation. This unit is called radian.
In addition, instead of calculating for approximated values (such as 57.29), we can just leave the exact values. For example, at (-1,0), the point is rotated half the distance on the circumference so it is radians. Halfway between (1,0) and
is
radians. At (0,-1) which is
radians.