Understanding Radian Measure
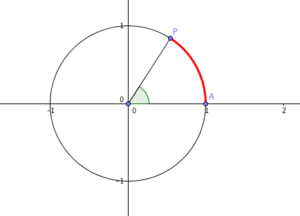
A circle O with radius 1 unit has its center placed at the origin. Let A be its intersection with the x-axis at (1,0) and P be another point on its circumference. If we move P along its circumference, then we can determine the distance traveled by P. If we let A be the starting point of P as it moves counterclockwise, then the distance traveled by P is equal to the length of arc AP represented by the red arc in the following figure.
To be able to know the length of arc AP, first, we must know the total distance traveled by P from A going counterclockwise and back to A (i.e. complete revolution). That is, we need to find the circumference of the circle. Since a unit circle has radius 1 unit, its circumference C is » Read more