The Dancing Triangle and Its Applications
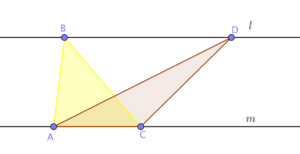
In the figure below, lines l and m are parallel lines. What can you say about the areas of triangle ABC and triangle ADC?
The distance between two parallel lines is equal at any point, so the two triangles have the same altitude (can you see why?). Further, the two triangles have a common base, therefore, their base lengths are equal. So, the areas of the two triangles are equal. In fact, you can choose any point P on line l and the areas of the triangle ACP will always equal to the areas of triangles ABC and ADC. We like to call this triangle the dancing triangle because using an applet, you can dance it by moving P without changing the area. In the applet below, move points B and D to dance the triangle.
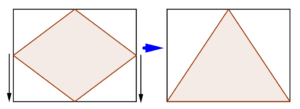
The dancing triangle may also be used to investigate the area of a parallelogram inscribed in a rectangle whose opposite vertices are fixed on the midpoint of the sides of the rectangle such as shown in the next figure. One of the ways to relate the area of the parallelogram to the area of the rectangle is to slide the opposite vertices to the same direction until they reach the vertex of the rectangle. After sliding, the resulting figure is a triangle. Since sliding the vertices does not change the area of the parallelogram (can you see why?), the area of the triangle which equals the area of the parallelogram is half that of the area of the rectangle. Of course, there are other ways that the two areas may be related and I encourage you to find as many as you can.
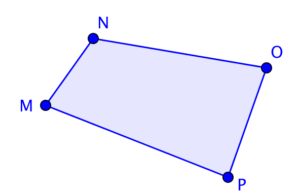
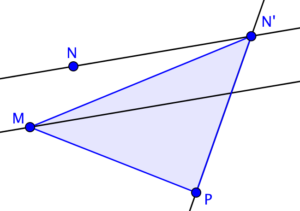
Another way to use the area of the dancing triangle is to form a triangle with the same area as a given quadrilateral (or vice versa). Suppose we want to form a triangle with the same area as quadrilateral MNOP.
To form the triangle, we can do the following.
1.) Draw diagonal MO.
2.) Draw a line parallel to MO and passing through N.
3.) Slide N to N’ such that PON’ forms a straight line.
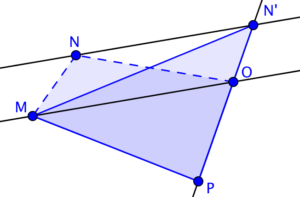
The triangle formed using this method is shown in the next figure.
As you can see, the area of triangle MNO is equal to the area of MN’O, so the area of the quadrilateral was not changed.
From above, we have shown that the area of triangle MN’P is equal to the area of quadrilateral MNOP.