The Dancing Triangle and Its Applications
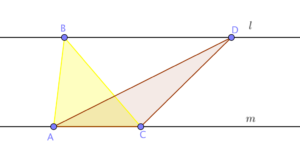
In the figure below, lines l and m are parallel lines. What can you say about the areas of triangle ABC and triangle ADC?
The distance between two parallel lines is equal at any point, so the two triangles have the same altitude (can you see why?). Further, the two triangles have a common base, therefore, their base lengths are equal. So, the areas of the two triangles are equal. In fact, you can choose any point P on line l and the areas of the triangle ACP will always equal to the areas of triangles ABC and ADC. We like to call this triangle the dancing triangle because using an applet, you can dance it by moving P without changing the area. In the applet below, move points B and D to dance the triangle. » Read more