combination math help Archives - Math and Multimedia

Introduction to Combinations

January 2, 2010 GB College Mathematics, Combinatorics, High School Algebra

Introduction to Combinations

In my Introduction to Permutations post, we have learned that the number of permutations (or arrangements) of $n$ objects taken at $n$ at a time written as $P(n,n)$ is equal to $n! = n(n-1)(n-2) \cdots (3)(2)(1)$ , and we have also learned that the number of permutations of $n$ objects taken $k$ at a time written as $P(n,k)$ is equal to $\displaystyle\frac{n!}{(n - k)!}$ .

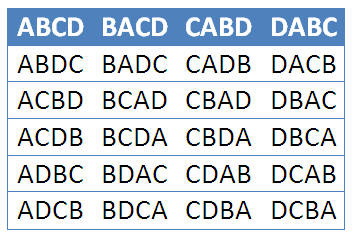
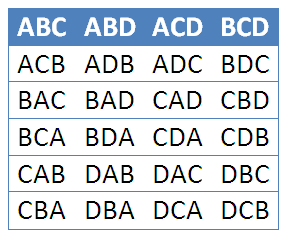
In Figure 1, shown are the permutations of $4$ letters, A, B, C and D taken $4$ at a time. From the figure, we can see that there are indeed $4!= (4)(3)(2)(1) = 24$ of such arrangement. In Figure 2, shown are the permutations of $4$ letters taken $3$ at a time, and we have shown that the number of permutations is equal to $\displaystyle\frac{4!}{ (4 - 3)!} = \frac{4!}{1!} = (4)(3)(2)(1) = 24$ . In Figure 3, we have again listed the permutations of $4$ letters taken $2$ at a time, and have shown that the number of permutations is equal to $\displaystyle\frac{4!}{(4-2)!} =12$ .

Figure 1 – Permutations of ABCD, taken 4 at a time.

Figure 2 – Permutations of ABCD, taken 3 at a time.

Figure 3 – Permutations of ABCD, taken 2 at a time.

If we talk about combinations, however, the arrangement of objects does not matter. For example, if we want to buy a milk shake and we are allowed to choose to combine any $3$ flavors from Apple, Banana, Cherry and Durian*, then the combination of Apple, Banana and Cherry is the same as the combination Cherry, Apple, Banana.

Try to list all the possible combinations of $3$ flavors taken from $4$ before proceeding.

If we choose to shorten the name the fruits by selecting the first letter of their names, we only have $4$ possible combinations for question above: ABC, ABD, ACD, and BCD. Notice that these are the only possible combinations. Also, observe that if we list the permutations of ABC, we have ACB, BAC,BCA, CAB and CBA. This means that in permutations, we have counted each combination of $3$ flavors from $4$ flavors $6$ times (or $3!$ times instead of one.

In other words, a combination is just like a subgroup of a group. For instance, if we want to find the number of subgroups containing $3$ objects taken from $4$ objects (or the combination of $4$ objects taken $3$ at a time), it is the same as asking “how many possible groups of $3$ objects can be taken from $4$ objects?” In Figure 4, all the possible subgroups of $3$ letters taken from $4$ letters are displayed by the orange border. You also would have realized that the number of permutations is an overcounting of the number of combinations.

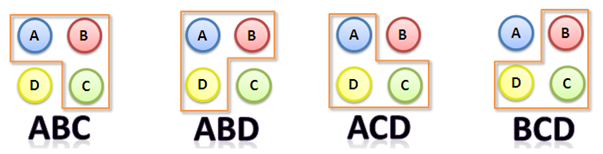
Figure 4 – The combinations of 4 objects taken 3 at a time is the same as the number of subgroups of 3 objects taken from 4 objects.

In Figure 2, ABC, ACB, BAC, BCA, CAB and CBA are permutations of Apples, Banana and Cherry. For each subgroup of $3$ , we realized that we counted $3! = 6$ times. So, to get the number of combinations, we divide our number of permutations $P(4,3)$ by the number of permutations of our subgroup $P(3,3) = 3!$ . Therefore, we can say that the number of combinations of $4$ objects taken $3$ at a time is equal to

$\displaystyle\frac{P(4,3)}{P(3,3)} = \frac{\frac{4!}{(4-3)!}}{3!} = \frac {4!}{(4-3)! 3!}$

In general, to get the number of combinations of $n$ objects taken $k$ at a time, we have to divide the number of permutations of $P(n,k)$ by the number of permutations of the subgroup $P(k,k)$ .