GeoGebra Basic Construction 2 – Isosceles Triangle
There are many ways to construct an isosceles triangle using GeoGebra. The concept in this construction is mathematical, so making a similar construction in other dynamic geometry software is more or less the same. Some geometry software will probably differ a little bit which will depend on how the tools are used in construction.
In this tutorial, we learn one way: To create a circle and use the center of the circle and two points on its circumference to form an isosceles triangle.
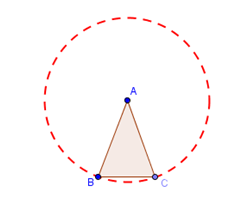
Figure 1 – Isosceles Triangle ABC.
The idea is to create a circle with radius AB, create point C on the circle and connect the vertices with the Polygon tool. The last step is to hide the circle. If you have used GeoGebra before, then this will be very easy.
| 1.) Open GeoGebra and select Geometry from the Perspectives menu in the Sidebar. | |
| 2.) Click the Circle with Center through Point tool and click two distinct places on the Graphics view to construct a circle with center A and passing through point B. | |
| 3.) If the labels of the points are not displayed, click the Move tool, right click each point and click Show label from the context menu. Notice that GeoGebra automatically names the points in alphabetical order. | |
4.) Select the Point tool and click the circumference of the circle to construct point C.
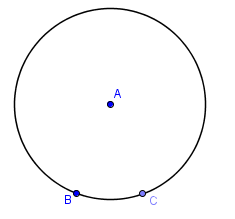 Figure 2 – Circle with center A and passing throught points B and C. |
|
| 5.) Drag the three points and observe the difference among the three. What do you observe? | |
| 6.) To draw the triangle, click the Polygon tool, click point A, click point B, click point C and click point A again to close the polygon. | |
|
|
7.) Next, we hide the circle by right clicking its circumference and unchecking Show Object from the context menu. |
| 8.) Drag the vertices of the triangle. What do you observe? Why is triangle ABC and isosceles triangle? |
Point C is an example of dependent objects in GeoGebra. Unlike points A and B, point C can only move along the circumference of the circle. Hence, AC will depend on the length of radius AB. In addition, since point C is dependent on the circumference of the circle, once you delete the circle, point C will also be deleted. This is not the same the other way around. Even if you delete point C, the circle will still remain.
Points A and B, on the other hand, are independent objects. Independent objects are not “attached” to other objects. You can drag them anywhere without restrictions.
If you have used GeoGebra before, it is possible to construct an isosceles triangle in other ways. Some of the tools that you can use are:
- Angle Bisector tool
- Perpendicular Bisector tool
- Midpoint tool
- Compass Tool