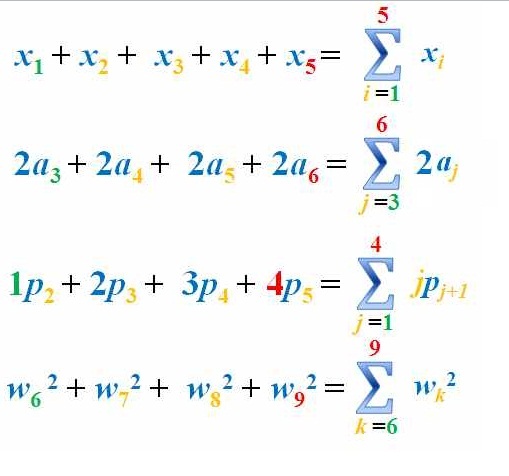How to use the summation symbol
If we want to add the expression all the way up to
, it is quite cumbersome to write
. Mathematical notations permit us to shorten such addition using the
symbol to denote “all the way up to” or “all the way down to”. Using the this symbol, the expression above can be written as
.
There is, however, a more compact way of writing sums. We can use the Greek letter as shown below.
In the figure above, a is the first index, and letter b is the last index. The variable(s) are the letters or the numbers that appear constantly in all terms. In the expression
is the first index,
is the last index and
is the variable. We use the letter
as our index variable, or the variable that will hold the changing quantities. Hence, if we are going to use the sigma or the summation notation for the expression
, we have
Some of the examples are shown below. Observe the colors of the indices and the variables, to familiarize yourself how the summation symbol works.
In using the summation symbol, take note of the following:
- An index variable is just a “dummy” variable. It means that you can use a different index variable without changing the value of the sum. The sum
is the same as
and is the same as
.
- The indices are the natural numbers
and so on.
- The last index is always greater than the first index.
- A variable without an index most of the time represent an infinite sum or a sum from
through
More Examples
| 1. | ||
| 2. | ||
| 3. | ||
| 4. | ||
| 5. |
Properties of the Summation Symbol
1.) The expression equals
which means that
. In general,
.
2.)The expression . Regrouping the expression, we have
. This means that
Generalizing, we have
3.) The expression (
of them)
. But
(
of them)
. Therefore,
.
4.) The expression . But
. In general,
.