GeoGebra Tutorial: Graphs and Sliders Part 2
In my post Tutorial 4: Graphs and Sliders, we learned how to use the slider in investigating graphs of the form y = mx + b. In this tutorial, we are going to use sliders to investigate the graph of the fromy = a(x – h)2+ k, where a, h and k can be any real number. We will first input the values of a, h and k in the input box before creating the sliders.
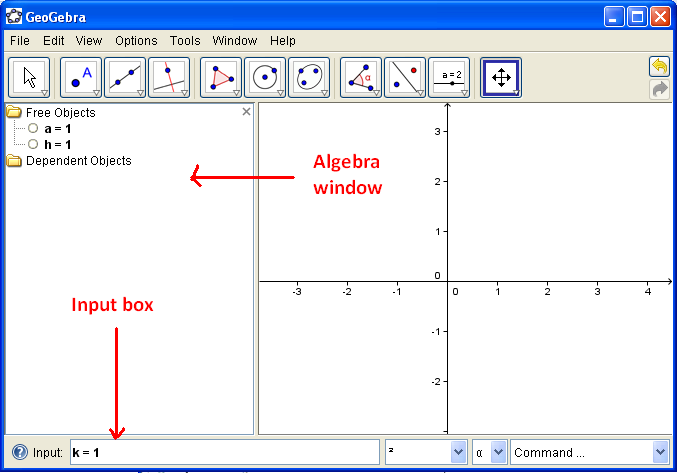
To do this, first we are going to assign temporary values for a, h and k in the input box, then create a slider for each of them. After creating a slider, we enter the equation y = a(x – h)2+ k in the input box to graph our function. You may want to look at our expected output here.
Instructions
- Open GeoGebra.
- Enter the following equations in the input box: a = 1, h = 1 and h = 1 in the Input box and press the ENTER key on your keyboard after typing each equation. Observe that the equations appear in the Free Objects section of the Algebra window.
- Right click each equation and click Show Object. Notice that the sliders appear in your drawing box.
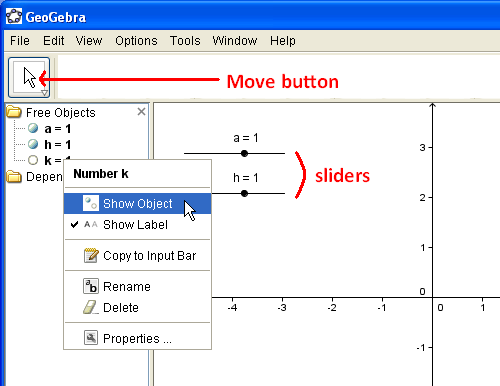
Figure 2 – Sliders are made by right-clicking each equation and pressing the Show Object option in the context menu.
- Type the equation y = a*(x – h)^2 + k, the press the ENTER key. If you have typed the equation correctly, a graph should appear in your drawing pad.
Q1: Click the Move button and move the small circle on your slider. What do you observe?
Q2: What are the effects of the parameters a, h and k to the graph of the function y = a*(x – h)^2 + k?