GeoGebra Tutorial 2 – Constructing an Equilateral Triangle
This is the second tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, please read the GeoGebra Essentials Series. This tutorial, answers the following problem using GeoGebra.
Note: This tutorial has been updated for GeoGebra 4.2.
In the tutorial below, menu commands, located in the menu bar, are in brown bold text, and submenus are denoted by the > symbol. For example, Options>Labeling> New Points Only means, click the Options menu, choose Labeling from the list, then select New Points Only. The GeoGebra tools are denoted by orange texts. For example, New Point means the new point tool.
Problem: How will you draw an equilateral triangle without using the Regular Polygon tool?
In this tutorial, we mimic compass and straightedge construction using the circle tool. The idea is to use one of the intersections of two circles and the two centers to form an equilateral triangle as shown in Figure 1.
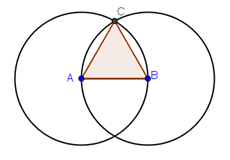
Figure 1 – An equilateral triangle formed by radii of two circles
In constructing the triangle, we learn how to use the circle tool, and how to display interior angle measure of a polygon and length of segments. Note that we can also draw a regular polygon of any side by using the Regular polygon tool. The output of this tutorial can be viewed here.
| 1.) Open GeoGebra, and then select Geometry from the Perspective panel in the Sidebar. | |
| 2.) Click the Segment between Two Points tool, and click two distinct places on the Graphics view to construct segment AB. | |
| 3.) If the labels of the points are not displayed, click the Move tool, right click each point and click Show label from the context menu. | |
4.) To construct a circle with center A passing through B, click the Circle with Center through Point tool, click point A, then click point B. Your drawing should look like the one shown in Figure 2.
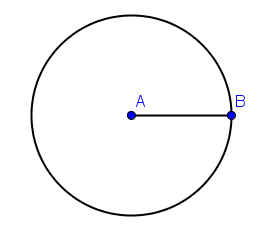 Figure 2 – Circle with center A and passing through B. |
|
|
|
5.) To construct another circle with center B passing through A, with the Circle with Center though Point still active, click point B and then click point A. |
| 6.) Next, we have to ‘intersect’ the circles. To intersect the two circles, select Intersect Two Objects, then click the circumference of both circles. Notice that two points appear in their intersections. After step 6, drawing should look like the one shown in Figure 3. | |
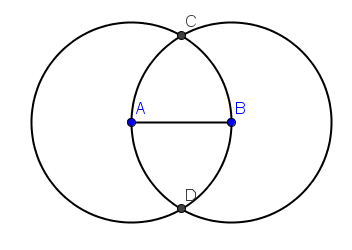 Figure 3 – Circles with radius AB and intersection Cand D. |
|
| 7.) We only need three points, points A, B and C, to form an equilateral triangle, so we hide the two circles, segment AB (be sure not to click points A or B when hiding) and point D. To do this, right click each object and click Show Object. | |
8.) With only three points remaining on the Graphics view, click the Polygon tool and click the points in the following order: A, B, C and then click A to close the polygon. After step 8, your drawing should look like the Figure 4.
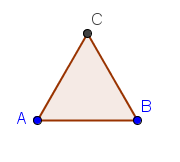 Figure 4 – Triangle formed from radii of two circles |
|
| 9.) Using the Move tool, move the vertices of the triangle. What do you observe? | |
| 10.) You have probably observed that ABC is an equilateral triangle. In fact, it is. To verify, we can display the interior angles of the triangle. To do this, click the Angle tool, then click the interior of the triangle. | |
| 11.) What do you observe? Move the vertices of the triangle. Is your observation still the same? | |
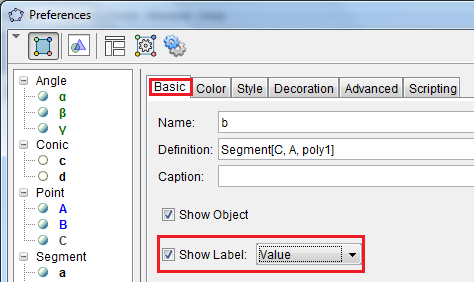
| 12.) You can also verify the length of the sides using the Preferences window. To do this, right click one of the sides of the triangle, click Object Properties from the context menu. | |
| 13.) In the Preferences window, select the Basic tab. Be sure that the Show label check box is checked and choose Value from the Show label drop down list box. | |
| 14.) Select the other sides of the triangle in the Object list located at the left side of the Preferences window and change the labels to Value, then close the window when you are done. | |
| 15.) Prove that the construction above always results to an equilateral triangle. |