This is the sixth tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, please read the GeoGebra Essentials Series.
In this tutorial, we are going to learn the following:
- use variables in GeoGebra
- compute using these variables
- use variables as parameters of objects
Problem: Given a rectangle with perimeter 10 units, find the dimension of the rectangle that can be formed that has the largest area.
This problem can be easily solved algebraically, but we are going to use GeoGebra to parameterize the length and the area of the rectangle to find its maximum area. The output of this tutorial is shown above.
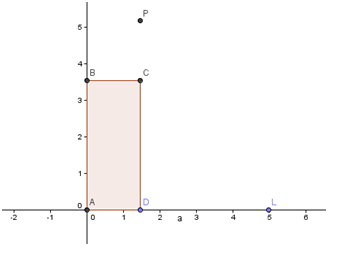
Figure 1 – Rectangle ABCD with two of its sides on the x and y-axis
Before doing the tutorial, let us first solve the problem. We know that the rectangle’s perimeter is constant, so we choose the width w. It follows that the height h will depend on the width. For instance, if w=4 units, then h = (10 – 2*4)/2 which is equal to 1. Hence, h = (10 – 2w)/2. Using this information, we plan the GeoGebra construction.
- First we make our maximum width 5 (Why?). We will create segment AL with length 5 with A at the origin and L at (5,0)
- Next, we create point D on AL. With D = (w,0), AD will be the width of the rectangle.
- We compute for h = (10 – 2w)/2, then, and take the value as the height of the rectangle. Then, we create point B with coordinates (0,h).
- We create the fourth vertex of the rectangle by getting the intersection of the horizontal line passing through B and a vertical line passing through D.
- Lastly, create ABCD using the polygon tool, and then produce point P (w, A_r) where A_r is the area of the rectangle.
Instructions
|
1.) Open GeoGebra and be sure that the Algebra & Graphics view is selected in the Perspectives panel. |
 |
2.) Select the Segment between Two Points tool, click on (0,0) and click on (5,0) to construct segment AB. Show the label of the points, and rename point B to L. |
 |
3.) Create a point on AL. You may not see the segment, so before doing this, hide the axes by clicking the Axes icon in the upper left of the Graphics View. If the icons are not displayed, click the arrow. |
 |
4.) Rename the recently created point to D. Move the point and notice that it can only move between A and L. Now, hide point L and display the axes. AD will be the width (lower base) of the rectangle. |
|
5.) We now determine the width and the height of the rectangle. First, we want to determine the AD which is the width. To do this, we get the x-coordinate of D (Why?). To get the x-coordinate of D, type w = x(D) in the Input bar and press the ENTER key. This means that the value of w, a declared variable, will be the x-coordinate of point D which is the same as the length of AD. |
|
6.) Next, we compute for the height h of the rectangle. Type h = (10 – 2w)/2 in the input bar and press the ENTER key. Notice the values of h and w were added to the Algebra view. |
|
7.) Next we create point B with coordinates (0,h). To do this, type B = (0,h) in the Input bar and press the ENTER key. This will be the third point on the rectangle. |
|

|
8.) Move point D. What do you observe? |
|
9.) Next, we locate the fourth vertex of the rectangle. The fourth vertex C will have the y-coordinate the same as B and x-coordinate the same as D. Therefore, we type C = (x(D), y(B)).
|
 |
10.) Now, we use the polygon tool to construct rectangle ABCD. Click the Polygon tool and then click the points in following order: point A, point B, point C, point D and, again, point A to close the figure. |
|
11.) Now, let us display the area of the polygon. Right click the interior of the rectangle, then click Object Properties to open the Preferences window. In the Basic tab of the Preferences window, check the Show Label check box and choose Value from the drop down list box. Close the window. |
|

|
12.) Move point D. What do you observe? What length of AD gives the rectangle the largest area? |
|
13.) Now, we create point P, type P = (w, poly1). Note that poly1 is the name of the rectangle and its value is area of the rectangle (see the Algebra view). |
|
14.) Right click on point P, then click check Trace On. This will trace the path of point P. |
|

|
15.) Move point D. What do you observe? What can you say about the curve formed by the traces of point P? Explain why your observations are such. |
|
16.) Solve the problem algebraically. What is the relationship between the equation formed from getting the solution of the problem and curve formed by traces of point P? |
