Tag: maximum area

Derivative and the Maximum Area Problem

Calculus and Analysis, College Mathematics, High School Calculus

Note: This is the third part of the Derivative Concept Series. The first part is The Algebraic and Geometric Meaning of Derivative and the second part is Derivative in Real Life Context.

Introduction

The computation of derivative is often seen in maximum and minimum problems.  In this article, we will discuss why do we get the derivative of a function and equate it to 0 when we want to get its maximum or minimum. To give you a concrete example, let us consider the problem below.

Find the maximum area a rectangle with perimeter 10 units.

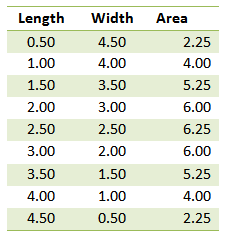
Without using calculus, we can substitute values for the rectangle’s length, compute for its width and its corresponding area. If we set the interval to 0.5, then we can come up with the table shown in Figure 1.

Figure 1 - Table showing the length, width, and area of a rectangle with perimeter 10.

Looking at the table above, we can observe that a rectangle of length of 2.5, a square, has the maximum area. If we have prior calculus  knowledge, however, we know that whatever the value of our perimeter, a square having the given perimeter will always have the maximum area.

Using elementary algebra, if we let x be the width of our rectangle, it follows that the length is 5-x. Let f(x) be the area of the rectangle. In effect, the area of the rectangle is described by the equation f(x) = 5x - x^2. We want to maximize the area, which implies that we want to find the maximum value of f(x).

Figure 2 – A rectangle with Perimeter 10 and width x units.

In elementary calculus, to compute for the maximum value of f(x), we get its derivative, which is equal to 5 - 2x, which we will denote f'(x). We then equate the f'(x) to 0 resulting to the equation 5-2x=0 \Rightarrow x = 2.5 which is exactly the maximum value in the table above.

Derivative and Equation to 0

In the article the Algebraic and Geometric Meaning of Derivative, we have learned that the derivative of a function is the slope of the line tangent to that function at a particular point. From elementary algebra, we also have learned the properties of slopes. If a line is rising to the right, the slope is greater than 0; if the line is rising to the to the left, then the slope is less than 0. We have also learned that a horizontal line has slope 0 and the vertical line has an undefined slope.

Figure 3 – Properties of slope of a straight line.

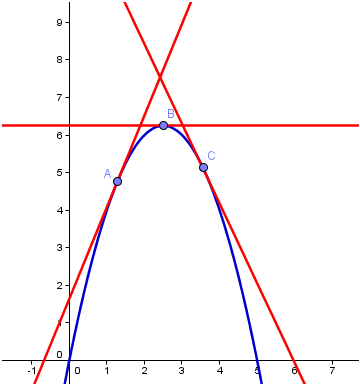
In the problem above, we calculated by getting the derivative (the slope of the line tangent to a function at a particular point) and equate it to 0. But a line with slope 0 is a horizontal line. In effect, we are looking for a horizontal tangent of f(x) = 5x-x^2. To give a clearer picture let us look at the graph of f(x) = 5x - x^2.

Figure 4 – Tangent lines of 5x – x2.

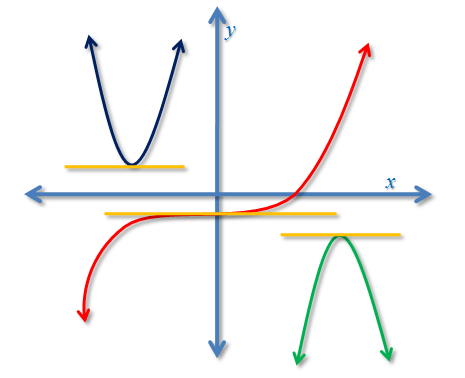
From the graph it is clear that the maximum point of the function is where the tangent line (red line) horizontal. In fact, there are only three possible cases that tangent line could be horizontal as shown in Figure 5: first, the minimum of a function (blue graph); second, the inflection point (red graph); and the third is the maximum of the function (green graph).

It should also be noteworthy to say that all the ordered pairs (length, area) or(width, area) in Figure 1 will be on the blue curve in Figure 4.

Figure 5 – Cases of a graph where the tangent is horizontal.

The derivative has many applications and it is seen in many topics in calculus.  In the next Derivative Tutorial, we are going to discuss how the derivative is used in other context.

Summary

  • The derivative of a function is the slope of the line tangent to a function at a particular point.
  • The horizontal line has slope zero.
  • In solving maxima and minima problems, we get the derivative of a function and equate to zero to get the minimum or maximum. We do this because geometrically, we want to get the line tangent to a function at a particular point that is horizontal.
2 comments , , , , , , , , , , ,

GeoGebra Tutorial 6 – Parameterization of Length and Area

GeoGebra, High School Mathematics, Software Tutorials

This is the sixth tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, please read the GeoGebra Essentials Series.

In this tutorial, we are going to learn the following:

  1. use variables in GeoGebra
  2. compute using these variables
  3. use variables as parameters of objects

Problem: Given a rectangle with perimeter 10 units, find the dimension of the rectangle that can be formed that has the largest area.

This problem can be easily solved algebraically, but we are going to use GeoGebra to parameterize the length and the area of the rectangle to find its maximum area. The output of this tutorial is shown above.

Figure 1 – Rectangle ABCD with two of its sides on the x and y-axis

Before doing the tutorial, let us first solve the problem. We know that the rectangle’s perimeter is constant, so we choose the width w.  It follows that the height h will depend on the width. For instance,  if  w=4 units, then h = (10 – 2*4)/2 which is equal to 1. Hence, h = (10 – 2w)/2. Using this information, we plan the GeoGebra construction.

  1. First we make our maximum width 5 (Why?). We will create segment AL with length 5 with A at the origin and L at (5,0)
  2. Next, we create point D on AL. With D = (w,0), AD will be the width of the rectangle.
  3. We compute for h = (10 – 2w)/2, then, and take the value as the height of the rectangle. Then, we create point B  with coordinates (0,h).
  4. We create the fourth vertex of the rectangle by getting the intersection of the horizontal line passing through B and a vertical line passing through D.
  5. Lastly, create ABCD using the polygon tool, and then produce point P (w, A_r) where A_r is the area of the rectangle.

Instructions

1.) Open GeoGebra and be sure that the Algebra & Graphics view is selected in the Perspectives panel.
2.) Select the Segment between Two Points tool, click on (0,0) and click on (5,0) to construct segment AB. Show the label of the points, and rename point B to L.
3.) Create a point on AL. You may not see the segment, so before doing this, hide the axes by clicking the Axes icon in the upper left of the Graphics View. If the icons are not displayed, click the arrow.
4.) Rename the recently created point to D. Move the point and notice that it can only move between A and L.  Now, hide point L and display the axes. AD will be the width (lower base) of the rectangle.
5.)  We now determine the width and the height of the rectangle. First, we want to determine the AD which is the width. To do this, we get the x-coordinate of D (Why?). To get the x-coordinate of D, type w = x(D) in the Input bar and press the ENTER key. This means that the value of w, a declared variable, will be the x-coordinate of point D which is the same as the length of AD.
6.) Next, we compute for the height h of the rectangle. Type h = (10 – 2w)/2 in the input bar and press the ENTER key. Notice the values of h and w were added to the Algebra view.
7.) Next we create point B with coordinates (0,h). To do this, type B = (0,h) in the Input bar and press the ENTER key. This will be the third point on the rectangle.

8.) Move point D. What do you observe?
9.) Next, we locate the fourth vertex of the rectangle. The fourth vertex C will have the y-coordinate the same as B and x-coordinate the same as D. Therefore, we type C = (x(D), y(B)). 
10.)  Now, we use the polygon tool to construct rectangle ABCD. Click the Polygon tool and then click the points in following order: point A, point B, point C, point D and, again, point A to close the figure.
11.)  Now, let us display the area of the polygon. Right click the interior of the rectangle, then click Object Properties to open the Preferences window. In the Basic tab of the Preferences window, check the Show Label check box and choose Value from the drop down list box. Close the window.

12.)  Move point D. What do you observe? What length of AD gives the rectangle the largest area?
13.)  Now, we create point P, type P = (w, poly1). Note that poly1 is the name of the rectangle and its value is area of the rectangle (see the Algebra view).
14.)  Right click on point P, then click check Trace On. This will trace the path of point P.

15.)  Move point D. What do you observe? What can you say about the curve formed by the traces of point P? Explain why your observations are such.
16.)  Solve the problem algebraically. What is the relationship between the equation formed from getting the solution of the problem and curve formed by traces of point P?
9 comments , ,