The Algebraic and Geometric Meaning of Derivative
Note: This is the first part of the Derivative Concept Series. The second part is Derivative in Real Life Context and the third part is Derivative and the Maximum Area Problem.
***
If we want to get the slope of a line, we need two points. Suppose the points have coordinates and
, we have learned that the slope is described by the formula
.
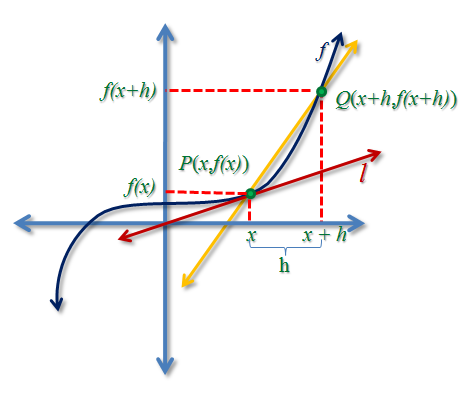
In Figure 1, we have line tangent to the function
at point
where the coordinates of
are
. The problem that gave birth to calculus is getting the slope of this tangent line. There is, however, a problem. We need two points to compute for the slope but we have only one point.
Note that the word tangent in this problem is different from the definition of tangent on a circle because it is clear that line will intersect the graph in more than one point.
Using the concept of limits we can remedy this problem. First, we create point with x coordinate
units to the right of the x-coordinate of
. We then draw line
, a secant line to the function
.
In effect, the coordinates of would be
and it is clear that the slope of the secant line
is described by the formula
If we want to approximate the slope of the tangent line, it is reasonable that we move towards
with
fixed. Click here to explore the diagram above using GeoGebra.
From the GeoGebra exploration above, if we move towards
, we observe the following:
1.) The value of approaches
.
2.) The inclination of the secant line approaches the inclination of the tangent line.
3.) The slope of the secant line approaches the slope of the tangent line.
4.) If point coincides with point
, then the slope of the secant line and is equal to the slope of the tangent line.
If we let be the slope of the secant line and
be the slope of the tangent line, focusing on observations 1 and 4, we can say the following equivalent statements:
- The limit of the slope of the secant line
as
approaches
is equal to
.
- The limit of the slope of the secant line
as
approaches
is equal to
.
- The limit of
as
approaches
is equal to
.
Using the limit notation, we can say that
From the above discussion, we can see that the derivative of a function at a particular point is the slope of the line tangent to that function at that particular point.
In the next post, we will discuss the meaning of derivative in real life situations.