Derivative in Real Life Context
Note: This article is the second part of the derivative concept series. The first part is The Algebraic and Geometric Meaning of Derivative and the third part is Derivative and the Maximum Area Problem.
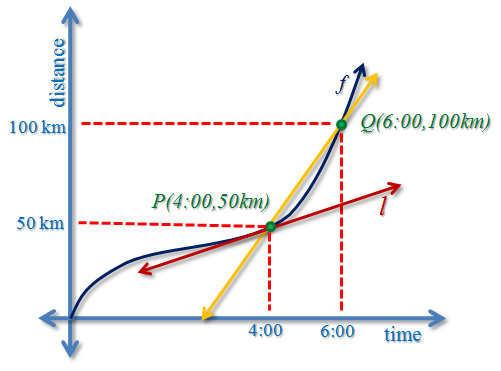
If we change the labels of the Figure 2 in the The Algebraic and Geometric Meaning of Derivative article – its x-axis to time and the y-axis to distance – the graph of the secant line is the difference in distance = 100 km – 50 km over the difference in time
= 10:00 – 8:00. This is shown in the figure below. This is equivalent to 50 km/2 hrs or 25 km/hr. From the computation above, it is clear that the interpretation of the slope of the secant line is the total distance over the total time or the average speed.
On the other hand, the slope of the tangent line is the speed of the bicycle at exactly 4 o’clock. At exactly 4:00 o’clock the bicycle was traveling 50 km per hour, a lot faster than its average speed. Now, this is reasonable because in real life, the speed of travel is not always constant. The slope of the tangent line or the speed of travel at a particular point is called the instantaneous speed.
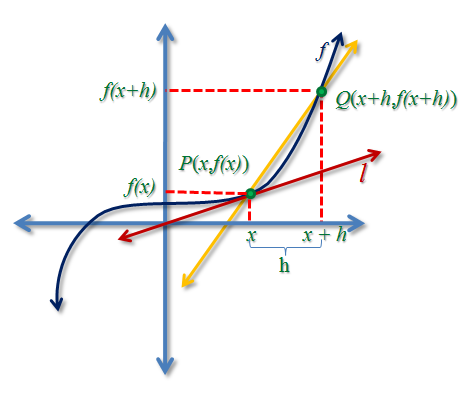
We have also observed from the previous article that as Q approaches P, the secant line’s approximation of the tangent line becomes better and better. This means that as Q approaches P, the average speed becomes closer and closer to the instantaneous speed at P.