Monthly Archives: April 2010

New GeoGebra Page

Posted on April 30, 2010 by Guillermo Bautista | 6 Comments

The GeoGebra complete List of Posts has been transferred to the GeoGebra page.

Tagged GeoGebra List of Tutorials, GeoGebra Tutorial Series, Mathematics and Multimedia GeoGebra

GeoGebra Tutorial 12 – Pictures and Angle Measures

Posted on April 30, 2010 by Guillermo Bautista | 10 Comments

This is the 12th tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, I strongly suggest that you read the GeoGebra Essentials Series.

In this tutorial, we learn how to use the Insert Image tool. We insert an image of a protractor in the GeoGebra Graphics view, create two connected segments, and measure the angles formed by two segments. We use the check box and the text tool to show or hide the actual measure to see if our approximation is correct. The final output of this tutorial is ideal for elementary school students for practicing their estimation skills on measuring angles.

In this tutorial, we learn the following:

Use new tools: The Insert Image and the Semicircle through Two Points tool.
Show/hide objects using a check box.
Combine the text and variable using the text tool to display measures of angles.

You can view the final output of the tutorial here and if you want to open GeoGebra in your browser and follow the instructions, click here.

Step-by-Step Instructions

	1. Open GeoGebra. We will need the Algebra view and the Axes so be sure that they are visible. If not, use the View menu from the menu bar to show them.
	2. We set GeoGebra to label new points only and not other objects. To do this, click the Options menu, click Labeling, then click New Points Only.
	3. Click the New Point tool, click the origin and click (12,0). Notice that GeoGebra automatically names the points in alphabetical order, the point in the orginin being A, and the other point being named as B.
	4. Click the Line through Two Points tool, click point A and then click point B.
	5. To create a semicircle passing through points A and B, click the Semicircle through Two Points tool click point A and click point B. Your drawing should look like Figure 1. Figure 1 – Semicircle passing through points A and B.
	6. To get the midpoint C of AB, select the Midpoint or Center tool, click point A and click point B.
	7. Now, we create two more points on the semicircle. To do this, select the New Point tool and click the on the circumference twice of the semicircle to produce points D and E.
	8. Now, create radii CD and CE by click the Segment between Two Points tool, click point C and click point D to connect CD. With the segment tool still active, click point C and point E to construct segment CE.
	9. To display the measure of angle DCE, select the Angle tool, click segment CE, then click segment CD. GeoGebra will automatically name DCEangle $\alpha$ . Figure 2 – Angle measure of DCE.
	10. Next, we hide the measure of angle DCE. To do this, click the Show/Hide Label tool, then click the angle measure (the green sector).
	11. Next, we hide points A and B and the semicircle. To do this, select the Show/Hide Object, click point A, point B, and the semicircle. Notice that all the clicked object are highlighted. Click the Move button to hide them.
	12. Now, let us insert the image of the protractor that we will use to measure the angle. To do this, select the Insert Image button, click anywhere on the Graphics view. In the Open dialog box, search and click the protractor image, click it and then click the Open button. This will display the protractor. Your GeoGebra window look like the one shown in Figure 3. Figure 3 – The Protractor image in the drawing pad.
	13. We now create a text that will display the measure of angle DCE. To do this, click the Insert Text tool, click anywhere on the drawing pad to display the text tool dialog box.
	14. In the Text dialog box, type the following: The measure of angle DCE is $\alpha$ is $\alpha$ The first $\alpha$ symbol can be inserted by selecting it in the Symbol drop down box (see figure) below the Edit box. This will display the Greek letter $\alpha$ . The second $alpha$ is the measure of the angle. It can be inserted using the Objects drop-down box. The second α will display the angle measure of DCE.
	15. Next, we will construct a check box that will display or hide the text that we have constructed. To do this, click the Checkbox to Show/Hide Objects tool and click anywhere on the Graphics view to display the check box dialog box.
	16. In the dialog box, type Show/Hide measure of angle DCE and choose Text Text1 from the Select objects… drop down list box, then click the Applybutton.
	17. Now, be sure that the Check box is uncheck to hide the angle measure of angle DCE. Move points D and E. Use the Move button to adjust the protractor to measure angle DCE. Guess the measurement of angle DCE. Figure 5 – Protractor measuring angle DCE.
	18. Click the check box to see if your approximation is near to the correct answer.

The protractor image used in this applet was from MathisFun.com. Before doing his tutorial, you need a picture of a protractor preferably in png format and with white background.

→ 10 Comments

Posted in GeoGebra, Software Tutorials

Tagged GeoGebra check box, geogebra insert image, GeoGebra semicircle, GeoGebra Tutorial Series, Geogegbra angle

Arithmetic Sequences and Linear Functions

Posted on April 28, 2010 by Guillermo Bautista | 13 Comments

Problem: Consider the diagrams below. If the pattern continues, how many squares will there be in Diagram 50? Diagram 100?

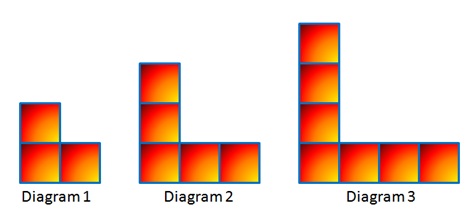
Figure 1 - A sequence of L-shaped square blocks.

In solving problems, it is important to present data in which we can easily see patterns. Table 1 shows the relationship between the diagram numbers and the number of squares.

Table 1 – The relationship between the diagram number and the number of squares.

We can solve this problem by “brute force” extending the table up to Figure 100, but that is not very “mathematical.” What mathematics had taught us is to find patterns, and, if possible, make generalizations. Using the first term, the constant difference and the diagram number, we can form a numerical expression that when simplified will result to the number of squares as shown in Table 2. Looking at the table, we can see that the first term is 3, and the difference is 2. Using this pattern, it is now easy to compute the number of squares of any diagram number.

Examine the table and see if you can find the pattern before proceeding.

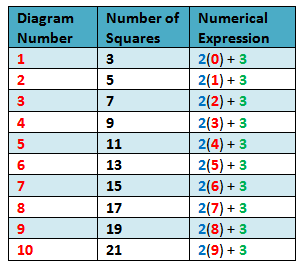
Table 2 - Numerical expressions describing the number of squares in each diagram number.

In Table 2, we can see that in the numerical expression column, the constant difference 2 and the first term 3 appear in every term. The changing quantity (variable) is the figure number - 1. Using the pattern, it is easy to see that the 50^th term is 2(50-1) + 3= 101 and the 100^th term is 2(100-1) + 3 = 201. In general, Figure n will have 2(n-1) + 3 = 2n + 1 squares.

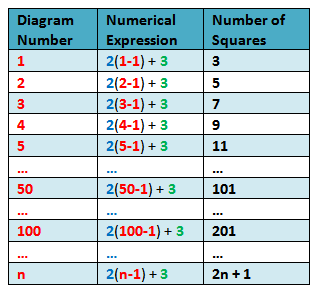
Table 3 – Generalized expression describing the number of squares.

Let us denote the nth term of a sequence by t_n. Since 2 and 3 are constants, if we let a be the first term of the sequence and d be the constant difference, then the formula that will describe the nth term of the sequence is

t_n = a(n-1) + d

Arithmetic Sequence as a Linear Function

Figure 2 shows the graph of the arithmetic sequence and its trend line denoted by the dashed line. Since we have a constant difference, we have a linear function. If we want to get the equation of the linear function that describes the relationship in our problem, since several ordered pairs are given, we can use the slope intercept formula.

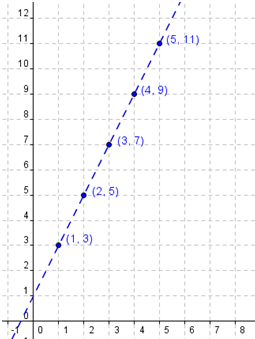
Figure 2 – Graph of the d(n) = 2n + 1, where d(n) is the diagram number

If we extend the trend line, it will pass the (0,1) (Why?). Getting (1,3) as our second point, the slope m will be (3-1)/(1-0) = 2. Hence, the equation of our line will be y = 2x + 1 which is of the same form as t_n = 2n + 1 in Table 3.