GeoGebra Essentials 1 – Locating a Triangle’s Centroid
This is the first tutorial in the GeoGebra Essentials Series. This tutorial will cater those who are new or those who have no knowledge in GeoGebra. If you are totally new to GeoGebra, it is important that you read the Introduction to GeoGebra post.
In the tutorial below, commands in the Menu bar are in bold green text and sub-menus are denoted by the > symbol. For example, Options>Labeling>New Points Only means, click the Options menu, choose Labeling from the list, then New Points Only. The tool texts are colored orange. For example, New Point means, the New Point tool.
In this tutorial, we create a triangle and find its centroid or the intersection of the medians. In doing the tutorial, we learn the following:
- Use the New Point, Segment Between Two Points, Midpoint or Center, Intersect two Objects and Move tools
- Learn how to Show/Hide Labels of objects
- Understand the difference between free and independent objects
Overview
First, we construct three points using the New Point tool and use the Segment between Two Points tool to connect these points which will be the vertices of the triangle. Then, we find the midpoint of each side using the Midpoint or Center tool. Next, we connect the three vertices to the midpoint of the opposite side. These segments are called medians of the triangle. We will observe and make conjectures about the characteristics of the medians.
The output of the tutorial is shown above. You may explore the applet before doing the tutorial.
Instructions
| 1. Open GeoGebra In this tutorial, we do not need the Algebra view and the Coordinate axes. To remove them, click Geometry from the Perspective panel in the Sidebar on the right part of the window. You can display the Perspective panel by clicking the arrow at the center right of the right border of the GeoGebra window. | |
| 2. To construct the vertices of the triangle ABC, click the New Point tool1, then click three different locations on the Graphics view. | |
| 3. To display the label of the points, select the Show/Hide Label button from the list under Move Graphics View button, then click the three points2. | |
| 4. Now, select the Segment between Two Points tool, then click point A and click point B to construct side AB. With the segment tool still active, click point B and click point C to construct BC. Now, construct side AC. | |
5. Select the Move tool and drag the points, labels, segments, and observe what happens. If you want to move the entire object, drag across the triangle to select it and move any of its parts. Your drawing should look like Figure 1.
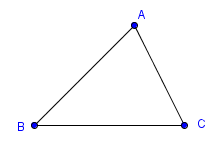 Figure 1 |
|
| 6. Next, we determine the midpoints of AB and AC. To get the midpoint of AB, select the Midpoint or Center tool, click point on A and click on point B. Next, with the midpoint tool still active, click on point A and click on point C to locate the midpoint of AC. Now, construct the midpoint of BC. | |
| 7. Use the Show/Hide Label tool to show the labels of points D, E and F, the midpoints of AB, AC and BC respectively. | |
8. Use the Segment betweenTwo Points tool, construct AF, BE and CD. After this step, your drawing should look like Figure 2.
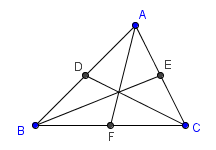 Figure 2 What do you observe about the triangle? |
|
| 9. Now, we intersect segments. To do this, select the Intersect Two Objects tool, then click the intersection of the three segments. This will produce point G, the point at the center of the triangle. | |
| 10. Use the Move tool to drag the vertices or sides of the triangle. Are your observations in 8 still the same? Make a conjecture about your observations. | |
| 11. Save your file by clicking File>Save on the menu bar. Name your file as essentials1. |
Notes:
1Notice that when you hover your mouse on the New Point tool, a tooltip on how to use it is shown on the toolbar. For instance, the direction for the New Point tool is “Click on the Graphics view, or on line, function or curve.” Use the description in exploring other tools later.
2By default, points are labeled in big letters and in alphabetical order.
Free and Dependent Objects
If you have observed, points A, B, C and can be moved using the mouse, but points D, E, and F cannot. That is because points D, E and F are dependent to other objects. Point D, for instance, is the midpoint of AB – meaning, point D will only move of point A or point B is moved. Point B cannot be moved once A and B are fixed.
GeoGebra classifies mathematical objects such as points, lines, polygons, etc. into dependent and free objects. In the example above, A, B and C are free objects; you can move them anywhere. Points D, E and F are dependent objects.
In the next tutorial, we learn more about free and dependent objects.
Last Update: October 13, 2015 (GeoGebra 5.0)