Equation of a line: The derivation of y = mx + b

March 18, 2011 GB High School Mathematics

We have discussed in context the origin (click here and here) of the linear equation $y = ax + b$ , where $a$ and $b$ are real numbers. We have also talked about the slope of a line and many of its properties. In this post, we will discuss the generalization of the equation of a line in the coordinate plane based on its slope and y-intercept.

We have learned that to get a slope of a line, we only need two points. We have also learned that given two points on a line, its slope is described as the rise (difference in the y-coordinates) over the run (difference in x-coordinates). Therefore, if we have two points with coordinates $(x_1,y_1)$ and $(x_2,y_2)$ , the slope $m$ is defined the formula

$m = \displaystyle\frac{y_2 - y_1}{x_2 - x_1}$ .

All the points on a vertical line have similar x-coordinates; therefore, the run ${x_2 - x_1}$ is equal to $0$ making $m$ undefined. From here, we can conclude a vertical line has no slope.

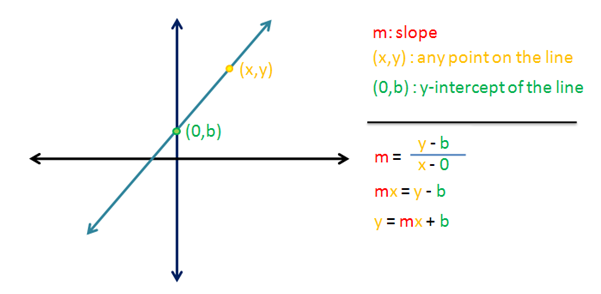
Now, it is clear that every non-vertical line has a slope (can you see why?). It is also clear that every non-vertical line will always pass through the y-axis — in fact, both axes. If we let $y = b$ be the y-intercept of line $l$ (see blue line below), then the coordinates of f that point are $(0,b)$ . If we choose any point on line $l$ with coordinates $(x,y)$ , then we can get the slope $m$ of the line passing through the two points as shown in the figure.

Therefore, the slope $m$ of any line passing through $(0,b)$ and $(x,y)$ is $y = mx + b$ . This is the general equation of a line given a point (on the line) and its y-intercept. This equation is called the slope-intercept form.

Related Articles

2 comments arithmetic sequence, arithmetic sequence equation, arithmetic sequence problems, equation of a line, graphing linear equation, linear equation, linear equation definition, linear equation example, linear function, linear function definition, linear function example, linear function graph, y = ax + b, y = mx + b

Equation of a line: The derivation of y = mx + b

Leave a ReplyCancel reply