GeoGebra Tutorial 28 – Animation and Hypocycloids
This is the 28th tutorial of the GeoGebra Intermediate Tutorial Series. If this is your first time to use GeoGebra, you might want to read the GeoGebra Essentials Series.
A hypocycloid is a special curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. It is comparable to the cycloid but instead of the circle rolling along a line, it rolls within a circle.
In the tutorial below, menu commands, located in the menu bar, are in green bold text, and sub-menus are denoted by the > symbol. For example, Options>Labeling> New Points Only means, click the Options menu, choose Labeling from the list, then select New Points Only. The tool texts are colored orange. For example, New Point means the new point tool. Texts typed in the input box are colored blue.
Instructions
| 1. Open GeoGebra and choose Algebra & Graphics from the Perspectives menu. | |
| |
2. First, we create point A at the origin by intersecting the x and y axes. To do this, select the Intersect Two Objects tool and then click on the x-axis, and then click on y-axis. |
| 3. Second, we construct a circle with center A and radius 3. We do this by typing circle[A,3] in the Input bar and pressing the ENTER key. | |
| |
4. Third, we construct point B in (3,0) using the New Point tool. |
| |
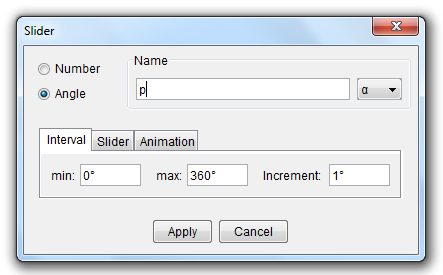
5. Neex, we rotate point B about point A using an angle slider and the rotate tool. To create an Angle slider, select the Slider tool and click on a vacant space in the Graphics view. This will display the Slider dialog box. |
| 6. In the Slider dialog box, select the Angle option button and change the Name of the angle to p as shown in the figure. Then select the Animation tab, change the Speed to 3, select Increasing from the Repeat box and then click the Apply button. Now, create another angle slider q with similar values.
|
|
| |
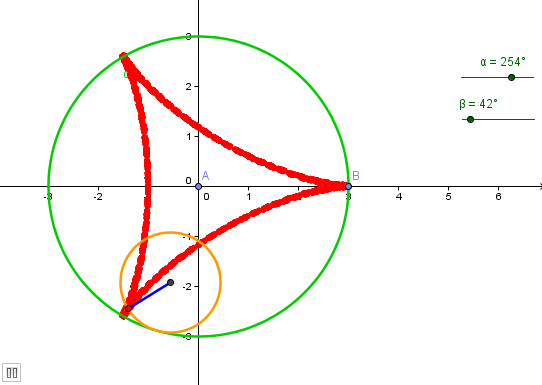
7. Next, we rotate point B about point A p degrees counterclockwise. To do this, select the Rotate Object around Point by Angle tool, click point B and then click point A to display the Rotate Object around a Point by Angle dialog box. |
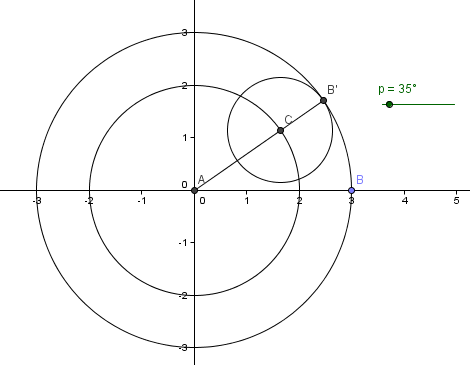
| 8. In the Rotate Object around Point by Angle dialog box, delete the text in the Angle text box and type p, choose the counterclockwise option, and click the OK button. This will produce another point B’ on the circle as shown below. | |
| 9. Next, we construct segment AB. The idea is to construct a circle with radius 2 and get the intersection of AB and that circle. That intersection D, will be the center of our rolling circle. | |
| 10. Type circle [A,2] and then use the Intersect Two Objects tool to intersect AB and the smaller circle. Your drawing should look like the figure below.
|
|
| 11. Next construct the circle centered at C and passing through B’. After this step, your construction should look like the Figure 4. | |
| 12. We now hide segment AB’ and the circle passing through point C. | |
| 13. We now create another slider that will rotate B’ clockwise about point C. To do this, create an angle slider q, set the animation speed to 9. Then rotate point B’ about C q degrees clockwise (refer to steps 5-8). This will produce point B”, the rotating point. | |
| 14. Next we hide B’ and turn on the animation. To hide B’, right click and then select Show label. To turn on the animation, right click the two sliders and select Animation on from the pop-up menu. Notice that a Pause button appears at the bottom-left of your Graphics view. | |
| 15. Next, Pause the animation by clicking the Pause button. Move both sliders to 0 and then Play the animation. | |
| |
16. Next, use the Segment Between Two Points tool and connect points B” and C. |
| 17. Now, color your hypocycloid as you please. |