Guest Post: Vedic Mathematics 4 – Nikhilam Method of Multiplication
Sanjay Guilati (author) has been teaching computer and mathematics in Bhilai, state Chattisgarh in India for 15 years. Currently he is a teacher in a senior secondary school and he is also involved in teacher training. His online work can be found in Mathematics Academy.
Multiplication – Nikhilam (निखिलम) Method
Conventional method of multiplication is time consuming. It involves number of steps and space. Multiplications done using Vedic Mathematics is easy, requires less number of steps, requires less time. One question can be solved in many ways and can be done mentally.
Nikhilam multiplication is one such method in which problems of special patterns can be solved in a step or two. For using this method, one must be familiar with the base system, which is described below.
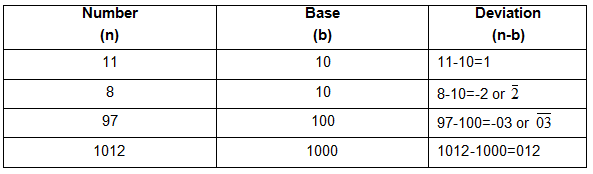
Base and Deviation: Ten and powers of ten are called bases. We will see in next post how other numbers can be taken as bases.
A number can be either less or more than the base. The difference between the number and base is known as deviation. Deviation may be positive or negative depending on the number being greater than or less than the base. Positive deviations are written without positive sign whereas the negative deviations are written with negative sign or with Rekhank (रेखांक), e.g.
Steps to be followed for multiplication
- The two numbers to be multiplied are written one below the other. Their deviations are written in front of the respective numbers.
- Answer space is divided into left hand side (LHS) and right hand side (RHS) by a slash.
- RHS of the answer is the product of the deviations of the numbers and will contain the digits equal to the number of zeroes of the base.
- LHS of the answer is the sum of one number with the deviation of the other.
- If RHS contains less number of digits than the number of zeroes in the base , the remaining digits are filled by giving zero or zeroes on the left side of RHS. If the number of digits are more than the number of zeroes in the base , the excess digit or digits are to be added to LHS of answer.
- Remove the slash to get the answer.
In general , if N1 and N2 are the two numbers near the same base and D1 and D2 are the their respective deviations from the base , then the operation of multiplication is carried out as follows:
Consider the following examples and the explanations below. Click the figure to enlarge.
Example 1
Step I : Here numbers (105 , 107) are near base 100. So RHS will have two digits. D1 x D2 = 05 x 07 = 35 (RHS)
Step II : (N1+D2) = 105 + 07 = 112 OR (N2+D1) = 107 + 05 = 112 (LHS)
Step III : Product 11235
Example 2
Step I : Here numbers (98 , 93) are near base 100. So RHS will have two digits. D1 x D2 = (-02) x(-07) = 14 (RHS)
Step II : (N1+D2) = 98 + (-07) = 91 OR (N2+D1) = 93 + (-02) = 91 (LHS)
Step III : Product 9114
Example 3
Step I : Here numbers (992 , 996) are near base 1000. So RHS will have three digits. D1 x D2 = (-008) x(-004) = 032 (RHS)
Step II : (N1+D2) = 992 + (-004) = 988 OR (N2+D1) = 996 + (-008) = 988 (LHS)
Step III : Product 988032
In the next post we will see how to multiply two numbers in which one number is more than and second number is less than the base.
Reference : Magical World of Mathematics
***
I have enjoyed reading each post on Vedic Mathematics by Sanjay Gulati, and I think most of you too. Vedic mathematics provides us with short-cuts for computations. This, of course, does not end there. The readers are encouraged to ponder upon, and find ways to understand (or better prove!) why these methods work. The proof would be another good post.
– Guillermo Bautista