Subset: a set contained in a set
Two weeks ago, we have talked about the basics of sets. In this post, we are going to talk about subsets.
In mathematics, if and
are sets, we say that
is a subset of
, denoted by
, if all elements of
are
also elements of
. The easiest way to illustrate this is through a Venn diagram as shown on the right. In the Venn diagram, set
is within set
. Therefore, all elements of set
are also elements of
.
Example 1
Let be set of all letters in the English alphabet and
be the set of vowel letters. It is clear that
since {a, e, i, o, u} are elements
and also are elements of
.
Example 2
If we let be the set of integers, and
be the set of even numbers, then
.
Example 3
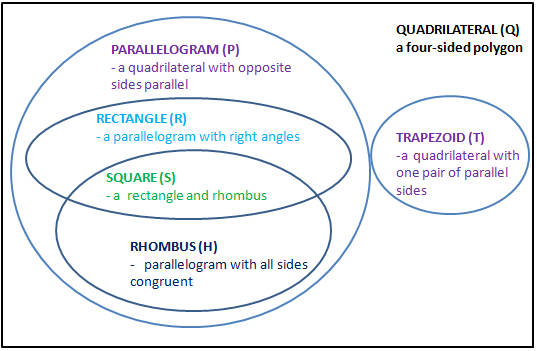
Let us examine the structure of quadrilaterals in the Venn diagram below.
From the diagram, it is clear that all squares are rectangles. If we let be the set of squares, and
be the set of rectangles, then
. We can also easily see from the diagram that the following statements are true:
,
, and
. Can you think of others?
Example 4
We also have talked about the structure of the real number system.
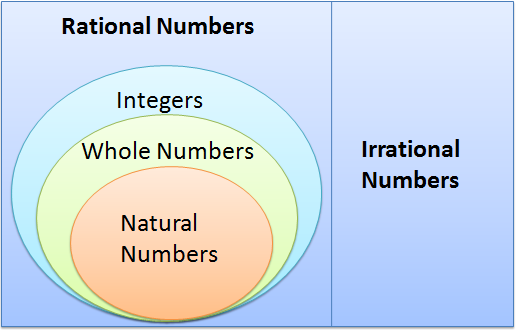
We have discussed and have shown that the following statements are true:
- The set of natural numbers
is a subset of whole numbers
.
- The set of natural numbers
is a subset of the integers
.
- The set of integers
is a subset of rational numbers
.
- The set of integers
is a subset of the rational numbers
.