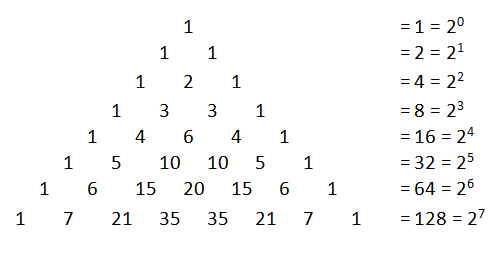Milkshakes and Power Sets
In Milkshakes, Beads, and Pascal’s Triangles, we have talked about a systematic way of choosing a combination of objects from a larger number of objects. Let us recall the problem in the said post.
Issa went to a shake kiosk and want to buy a milkshake. The shake vendor told her that she can choose plain milk, or she can choose to combine any number of flavors in any way she wants. There are four flavors to choose from: Apple, Banana, Chico, and Durian. How many possible combination of flavors can Issa make?
In the problem, Issa can choose any number of flavors and any combination. She can choose plain milk, choose one flavor at a time, two flavors at a time, three flavors at a time, or four flavors at a time as shown in the table below (click the table to enlarge).
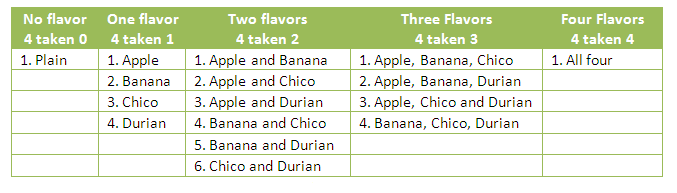
Notice that in writing the list, we have exhausted the number of subsets in a set with four elements. If we let a, b, c, and d stand for avocado, banana, chico, and durian, let them be members or a set and use the set notation, we can write the subsets as follows:
- set with 0 flavors: {}
- set with 1 flavor: {a} , {b}, {c}, {d}
- set with 2 flavor: {a, b} , {a, c}, {a, d}, {b, c}, {b, d}, {c, d}
- set with 3 flavors: {a, b, c } , {a, b, d}, {a, c, d}, {b, c, d}
- set with 4 flavors: {a, b, c, d}
In 1, no flavor was chosen so we have a set with no element. In mathematics, a set with no element is called the empty set. As we can see, there are 1 + 4 + 6 + 4 + 1 = 16 possible combinations.
We can also use combination in solving the problem because we are counting four flavors taken one at a time, two at a time, three at a time, and four at a time. Using the combination notation, we can write the computation above as
Now, how do we generalize the computation above? Given a set, how many subsets can we form? Let’s have a few cases.
For sets with 1 element, we have
For sets with 2 elements, we have
For sets with 3 elements, we have
Observe that the number of subsets above are , and
, which are all powers of 2:
,
,
,
, and
. If we extend our computation, we form the Pascal’s triangle, and we can see that if we extend this triangle downward, we can see that the sums are still powers of 2.
Note that if we can prove that the sums of all the rows in a Pascal’s triangle are powers of 2, we also prove that the numbers of subsets in a set are powers of 2. Therefore, we can conjecture that number of subsets in a set with elements is
. We will discuss the proof of this conjecture later.
The set of all subsets in a set including the empty set is called its power set. Hence, if we let P be the power set of {a,b,c,d}, then P = {{},{a} , {b}, {c}, {d}, {a, b} , {a, c}, {a, d}, {b, c}, {b, d}, {c, d}, {a, b, c } , {a, b, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}.