The 12 Days of Christmaths and the Triangular Numbers
Many of us are familiar with the Twelve Days of Christmas — a song that enumerates a series of increasingly grand gifts given on each of the twelve days of Christmas. For those who are not familiar with the song, here are a few stanzas (for full lyrics, click here).
On the first day of Christmas,
my true love sent to me
A partridge in a pear tree.
On the second day of Christmas,
my true love sent to me
Two turtle doves,
And a partridge in a pear tree.
On the third day of Christmas,
my true love sent to me
Three French hens,
Two turtle doves,
And a partridge in a pear tree.
On the fourth day of Christmas,
my true love sent to me
Four calling birds,
Three French hens,
Two turtle doves,
And a partridge in a pear tree.
The math: How many gifts was given on the twelfth day?
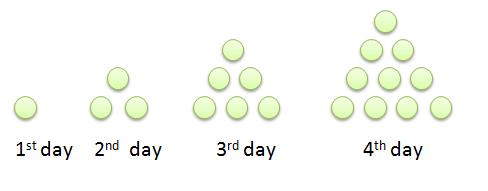
If we examine the song we have 1 gift on the first day, 3 gifts in the second day, 6 gifts in the third day, and 10 gifts in the fourth day. Note that the number of gifts can be represented as circles in triangular form. Since the numbers form a triangle, we call them triangular numbers or triangle numbers. The first four triangular numbers are 1, 3, 6, and 10. Based on the pattern, what are the next three triangular numbers?
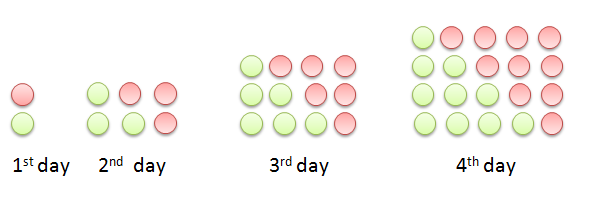
Using the representation above, we want to find the number of circles on the 12th day. This can be answered manually by drawing, but this will be quite a tedious task. We use a different strategy: we rearrange the circles so they form right triangles, and double them to form rectangular numbers.
Notice that on the first day, we have formed a 1 by 2 rectangle, on the second day, we have formed a 2 x 3 rectangle, and on the third day, we have formed a 3 by 4 rectangle. This means that on the twelfth day, we will have formed a 12 by 13 rectangle. Now that gives us 156 circles or 156 gifts. But recall that we have doubled the number of circles to form the rectangles. Therefore, we have to divide the result by 2. This gives us 78 gifts. So, on the twelfth day of Christmas 78 gifts were given by one’s true love.
Notice that the question above is similar to the following:
- What is the 12th triangular number?
- What is the sum of all the positive integers from 1 to 12?
- How many handshakes can be done with 12 people assuming that nobody handshakes with himself? (see The Handshake Problem and It’s Multiple Solutions).
The problem above can also be generalized. What is the nth triangular number? What is the sum of the numbers from 1 to n? How many handshakes can be made by n people in a party if one person handshakes with all of the persons in the party once?
From above, we can create an n by n + 1 rectangle. We divide the result by 2 since we have doubled the number of circles. Therefore, the number of gifts on the nth day is : .