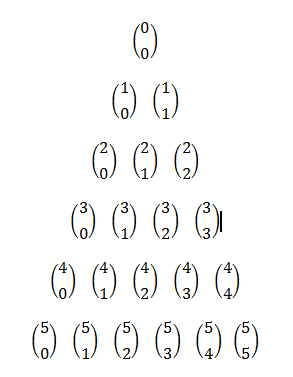Counting the Number of Subsets in a Set
Problem: How many groups can be formed from 5 persons?

First, we represent the persons by small letters a, b, c, d, and e, and we denote a group whose members are c and d as {c, d}. We can have a group with 2 members, 3 members, 4 members, and 5 members. The members in each group are listed below.
10 groups with two members in each group:
{a, b}, {a, c}, {a, d}, {a, e}, {b, c}, {b, d}, {b,e}, {c, d}, {c,e}, {d,e}.
10 groups with three members in each group:
{a, b, c}, {a, b, d}, {a, b, e}, {a, c, d}, {a, c, e}, {b, c, d}, {b, c, e}, {b, d, e}, {c, d, e}
5 groups with four members in each group:
{a, b, c, d}, {a, b, c, e}, {a, b, d, e},{a, c, d, e}, {b, c, d, e}
1 group with five members:
{a, b, c, d, e}
Therefore, 26 groups of at least two members, can be formed from 5 persons.
In set theory, we also talk about the number of groups in a group, or, technically, the number of subsets in a set. However, in this problem, the sets with 1 element and the set with no element (the empty set) are also counted. Therefore, aside from the sets listed above, we also include the following:
5 groups with one element: {a}, {b}, {c}, {d}, {e}
1 group with no element: {}
In effect, the number of sets in a set with 5 elements is 32.
Notice that in counting the number of subsets with 4 elements, we compute the number of combinations of 5 elements taken 4 at a time. So, in counting all the subsets, we find the the sum of 5 taken 0 at time, 5 taken 1 at a time, all the way up to 5 taken 5 at a time. The equivalent of that sum in symbol is
which is the sixth row of the Pascal’s Triangle shown below.
Obviously, in finding the number of subsets in a set with n elements, we have to add the number of subsets with 0, 1, 2, 3 all the way up to n-1 elements or
.
Looking at Pascal’s triangles, adding the numbers in each row gives us a sum of powers of 2. The number of subsets in a set with 2 elements is , the number of subsets in a set with 3 elements is
, the number of subsets in a set with 4 elements is
, and so on.
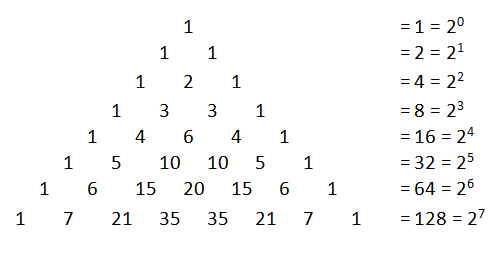
Generalizing the pattern above, the number of subsets in a set with elements is
.
In the “group problem,” we did not count the groups with 1 member (5 groups), and the groups with no member (the empty set). So, the number of groups that can be formed with 5 persons is . In general, the number of groups with at least 2 members that can be formed from
people is
.