Wedding Guests and Circular Permutations
In a wedding banquet, guests are seated in circular table for four. In how many ways can the guests be seated?
We have learned that the number of permutations of distinct objects on a straight line is
. That is, if we seat the four guests Anna, Barbie, Christian, and Dorcas, on chairs in on a straight line they can be seated in
ways (see complete list).
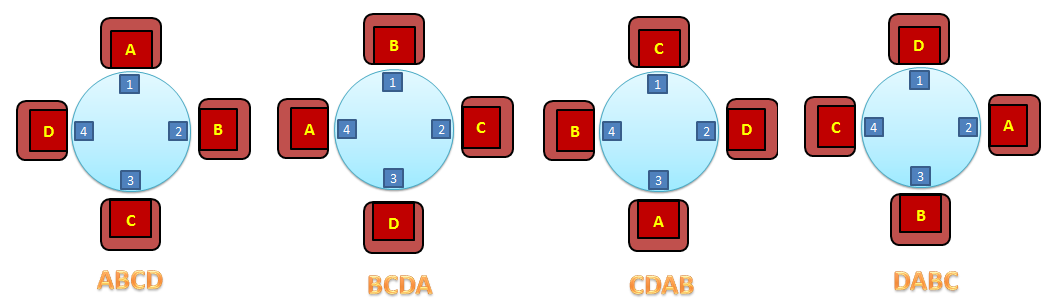
However, circular arrangement is slightly different. Take the arrangement of guests A, B, C, D as shown in the first figure. The four possible seating arrangements are just a single permutation: in each table, the persons on the left and on the right of each guest are still the same persons. For example, in any of the tables, B is on the left hand side of A and D is on the right hand side of A. In effect, the four linear permutations ABCD, BCDA, CDAB, and DABC are as one in circular permutation. This means that the number of linear permutations of 4 persons is four times its number of circular permutations. Since the number of all possible permutations of four objects is 4!, the number of circular permutations of four objects is .
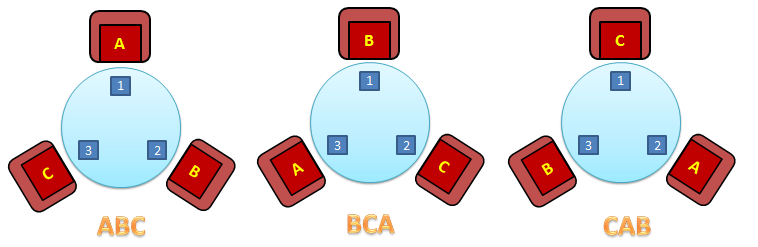
This is also similar with circular permutations of three objects. Since the number of permutations of three objects is , the number of circular permutations of three objects is
.
The observation above can be generalized. Notice that the circular permutations in both figures are just the rotations of the guests about the table. Rotating the guests without swapping their positions pairwise does not change the permutation since the person the right and left of each person will still be the same person after the rotation. This means that if there are 8 persons seated, they can be rotated 7 times giving us 8 possible seating arrangements (includes the initial position). So, we have circular permutations of 8 guests.
In general, given number of objects, there are
circular permutations.
But
.
Simplifying the equation above, we have
.
Therefore, the number of circular permutations of objects is
***
This post was brought to you by Amanda Green.