Wedding Guests and Circular Permutations
In a wedding banquet, guests are seated in circular table for four. In how many ways can the guests be seated?
We have learned that the number of permutations of distinct objects on a straight line is
. That is, if we seat the four guests Anna, Barbie, Christian, and Dorcas, on chairs in on a straight line they can be seated in
ways (see complete list).
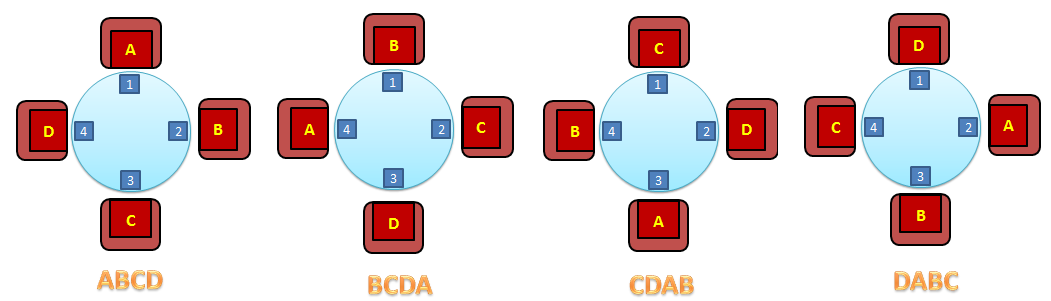
However, circular arrangement is slightly different. Take the arrangement of guests A, B, C, D as shown in the first figure. The four possible seating arrangements are just a single permutation: in each table, the persons on the left and on the right of each guest are still the same persons. For example, in any of the tables, B is on the left hand side of A and D is on the right hand side of A. In effect, the four linear permutations ABCD, BCDA, CDAB, and DABC are as one in circular permutation. This means that the number of linear permutations of 4 persons is four times its number of circular permutations. Since the number of all possible permutations of four objects is 4!, the number of circular permutations of four objects is . » Read more