A Simple Proof of the Arithmetic Mean Geometric Mean Inequality

May 16, 2012 GB High School Mathematics, High School Number Theory

Last February, we have used area to prove the Arithmetic Mean – Geometric Mean Inequality (AM-GM Inequality). In this post, we show a simpler proof.

Click image view the GeoGebra applet demonstration

Recall that the AM-GM Inequality states that given two numbers, their geometric mean is always less than or equal to their arithmetic mean. That is given two numbers $a$ and $b$ ,

$\displaystyle\sqrt{ab} \leq \frac{a+b}{2}$ .

Proof

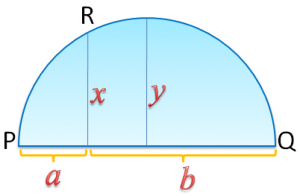
Consider the semicircle above with radius $y$ . If we construct any vertical segment $x$ from $PQ$ to a point on the semicircle, we are sure that its length is less than or equal to the length of radius. That is, we are sure that the following inequality always holds

$x \leq y$ .

The diameter of the circle is equal to $a + b$ , so its radius

$y = \displaystyle \frac{a + b}{2}$ .

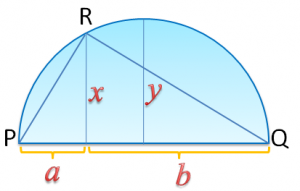
If we draw $PR$ and $QR$ , we form two right triangles that are similar, the triangle containing the sides $a$ , $x$ , and $PR$ , and the triangle containing the sides $x$ , $b$ , and $QR$ . In effect, since the two triangles are similar,