Deceptive and Misleading Mathematical Patterns

In the Mathematical Palette, I have mentioned about mathematics as a science of patterns. I have highlighted that some mathematical patterns are obvious, some can be solved mathematically, and some are a bit counter-intuitive.
In reality, we have improved our way of living by recognizing and generalizing patterns. For example, we are able to predict the weather through the data we have collected all over the years. We look for patterns from the data and use probability to announce that there will be rain showers and thunderstorms for the next three days and feel pretty sure about it. Through patterns, we have even predicted the movement of planets. We know that the next transit of Venus is in 2117 (too bad if you didn’t see it on June 5). That is how beautiful and powerful patterns are.
On the other hand, you cannot trust patterns all the time. The French mathematician Pierre de Fermat observed that the sequence
are prime numbers. The sequence can be expressed as where
, so he declared that all numbers of that form (now known as Fermat Numbers) are prime without bothering to check the next term. Leonhard Euler discovered that the next term of the sequence is composite. For
, we have
.
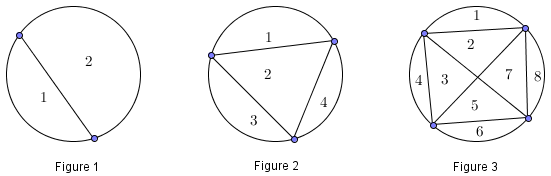
Another classic example of a misleading pattern is the maximum number of partitions in the interior of a circle formed by joining points on its circumference with a segment. Below, we see that Figure 1 has partitions, Figure 2 has
, Figure 3 has
and Figure 4 has
partitions.
Of course, it is very tempting to say that Figure 5 has partitions, but looking at the figure, we only have 31.
The patterns above only show that we cannot always trust what we see or observe. That is also one of the main reasons why mathematical proofs exist.