5 Fascinating Facts About Triangles That Will Surprise You
If you have enjoyed the wonders and beauty of mathematics shown in this blog, here are some addition for you to appreciate it more. Below are some of the most amazing facts about triangles.
1. The three altitudes of meet at a common point. This point is called the orthocenter of the triangle.
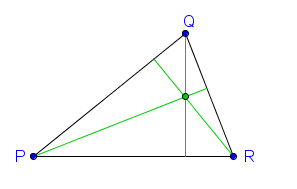
2. The three lines from each vertex to the midpoint of the opposite side also meet at a common point called centroid of the triangle. » Read more